| 次の(1)~(15)の中から,指示された8問について答えなさい。 |
| 1 |
 8+12÷(-4) 8+12÷(-4)
|
11 |
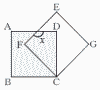 右の図のように,正方形ABCD,正方形EFCGがある。正方形ABCDを,点Cを中心として,時計まわりに45°だけ回転移動させると,正方形EFCGに重ね合わせることができる。このとき,∠xの大きさを求めなさい。 右の図のように,正方形ABCD,正方形EFCGがある。正方形ABCDを,点Cを中心として,時計まわりに45°だけ回転移動させると,正方形EFCGに重ね合わせることができる。このとき,∠xの大きさを求めなさい。
|
| 2 |
 12ab÷6a2×2b 12ab÷6a2×2b
|
| 3 |
 次の数の大小を,不等号を使って表しなさい。 次の数の大小を,不等号を使って表しなさい。
4 , √10 |
12 |
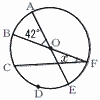 右の図で,6点A,B,C,D,E,Fは,円Oの周上の点であり,線分AEと線分BFは円Oの直径である。点C,点DはBEを3等分する点である。∠AOB=42°のとき,∠xの大きさを求めなさい。 右の図で,6点A,B,C,D,E,Fは,円Oの周上の点であり,線分AEと線分BFは円Oの直径である。点C,点DはBEを3等分する点である。∠AOB=42°のとき,∠xの大きさを求めなさい。
|
| 4 |
x=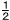 ,y=-3のとき,2(x-5y)+(2x+3y)の値を求めなさい。 ,y=-3のとき,2(x-5y)+(2x+3y)の値を求めなさい。
|
| 5 |
|
13 |
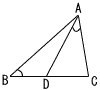 右の図のように,△ABCがあり,点Dは辺BC上にある。AB=12cm,AC=8cm,CD=6cm,∠ABC=∠DACのとき,線分ADの長さを求めなさい。 右の図のように,△ABCがあり,点Dは辺BC上にある。AB=12cm,AC=8cm,CD=6cm,∠ABC=∠DACのとき,線分ADの長さを求めなさい。
|
| 6 |
|
| 7 |
| 連立方程式 |
 |
2x+y=5 |
を解きなさい。 |
| x-4y=7 |
|
14 |
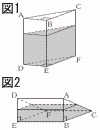  図1のように,三角柱ABC-DEFの形をした透明な容器に,水を入れて密閉した。この容器の側面はすべて長方形で,AB=6cm,BC=8cm,CF=12cm,∠ABC=90°である。この容器を,△DEFが容器の底になるように,水平な台の上に置いた。このとき,容器の底から水面までの高さは8cmである。この容器を図2のように,四角形FEBCが容器の底になるように,水平な台の上に置きかえたとき,容器の底から水面までの高さを求めなさい。ただし,容器の厚みは考えないものとする。 図1のように,三角柱ABC-DEFの形をした透明な容器に,水を入れて密閉した。この容器の側面はすべて長方形で,AB=6cm,BC=8cm,CF=12cm,∠ABC=90°である。この容器を,△DEFが容器の底になるように,水平な台の上に置いた。このとき,容器の底から水面までの高さは8cmである。この容器を図2のように,四角形FEBCが容器の底になるように,水平な台の上に置きかえたとき,容器の底から水面までの高さを求めなさい。ただし,容器の厚みは考えないものとする。 |
| 8 |
方程式 x2+5x+2=0 を解きなさい。
|
| 9 |
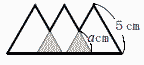 右の図のように,1辺の長さが5cmの正三角形の紙を,その一部が重なるように,横一列に3枚並べて図形をつくる。このとき,重なる部分は,すべて1辺の長さがacmの正三角形となるようにする。図の太線は,図形の周囲を表している。太線で表した図形の周囲の長さを,aを用いた式で表しなさい。 右の図のように,1辺の長さが5cmの正三角形の紙を,その一部が重なるように,横一列に3枚並べて図形をつくる。このとき,重なる部分は,すべて1辺の長さがacmの正三角形となるようにする。図の太線は,図形の周囲を表している。太線で表した図形の周囲の長さを,aを用いた式で表しなさい。 |
15 |
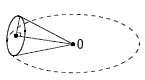 右の図のように,底面の半径が4cmの円錐を平面上に置き頂点Oを中心としてすべらないように転がした。このとき,点線で表した円Oの上を1周し,もとの場所にもどるまでに3回半だけ回転した。この円錐の表面積を求めなさい。ただし,円周率をπとする。 右の図のように,底面の半径が4cmの円錐を平面上に置き頂点Oを中心としてすべらないように転がした。このとき,点線で表した円Oの上を1周し,もとの場所にもどるまでに3回半だけ回転した。この円錐の表面積を求めなさい。ただし,円周率をπとする。
|
| 10 |
| nは100より小さい素数である。 |
231 |
が |
| n+2 |
整数となるnの値をすべて求めなさい。 |
 右の図のように,正方形ABCD,正方形EFCGがある。正方形ABCDを,点Cを中心として,時計まわりに45°だけ回転移動させると,正方形EFCGに重ね合わせることができる。このとき,∠xの大きさを求めなさい。
右の図のように,正方形ABCD,正方形EFCGがある。正方形ABCDを,点Cを中心として,時計まわりに45°だけ回転移動させると,正方形EFCGに重ね合わせることができる。このとき,∠xの大きさを求めなさい。 右の図で,6点A,B,C,D,E,Fは,円Oの周上の点であり,線分AEと線分BFは円Oの直径である。点C,点DはBEを3等分する点である。∠AOB=42°のとき,∠xの大きさを求めなさい。
右の図で,6点A,B,C,D,E,Fは,円Oの周上の点であり,線分AEと線分BFは円Oの直径である。点C,点DはBEを3等分する点である。∠AOB=42°のとき,∠xの大きさを求めなさい。 右の図のように,△ABCがあり,点Dは辺BC上にある。AB=12cm,AC=8cm,CD=6cm,∠ABC=∠DACのとき,線分ADの長さを求めなさい。
右の図のように,△ABCがあり,点Dは辺BC上にある。AB=12cm,AC=8cm,CD=6cm,∠ABC=∠DACのとき,線分ADの長さを求めなさい。
 右の図のように,1辺の長さが5cmの正三角形の紙を,その一部が重なるように,横一列に3枚並べて図形をつくる。このとき,重なる部分は,すべて1辺の長さがacmの正三角形となるようにする。図の太線は,図形の周囲を表している。太線で表した図形の周囲の長さを,aを用いた式で表しなさい。
右の図のように,1辺の長さが5cmの正三角形の紙を,その一部が重なるように,横一列に3枚並べて図形をつくる。このとき,重なる部分は,すべて1辺の長さがacmの正三角形となるようにする。図の太線は,図形の周囲を表している。太線で表した図形の周囲の長さを,aを用いた式で表しなさい。 右の図のように,底面の半径が4cmの円錐を平面上に置き頂点Oを中心としてすべらないように転がした。このとき,点線で表した円Oの上を1周し,もとの場所にもどるまでに3回半だけ回転した。この円錐の表面積を求めなさい。ただし,円周率をπとする。
右の図のように,底面の半径が4cmの円錐を平面上に置き頂点Oを中心としてすべらないように転がした。このとき,点線で表した円Oの上を1周し,もとの場所にもどるまでに3回半だけ回転した。この円錐の表面積を求めなさい。ただし,円周率をπとする。