全国公立高校入試 　１番問題　【令和４年春】

（２０）長野県

学習日　　　 月　　 　日（　　　）

印刷して、紙の上でやってネ！ 　印刷用

１	5＋(－2)	７	ことがらAの起こる確率がのとき,Aの起こらない確率を求めなさい。
２	(－6x＋9)÷3	８	√6の小数部分をaとするとき, a(a＋2)の値を求めなさい。
３	84nの値が,ある自然数の2乗となるような自然数nのうち,最も小さいものを求めなさい。	９	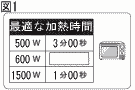電子レンジで食品を加熱するとき，電子レンジの出力をxW (ワット),最適な加熱時間をy秒とすると，yはxに反比例することがわかっている。あるコンビニエンスストアで販売されている弁当には,図1 のようなラベルがはってある。 　このとき,図1の□の中のに当てはまる最適な加熱時間を求めなさい。
４	二次方程式 x2＝4xの解として,最も正しいものを次のア～エから1つ選び,記号を書きなさい。 　ア　x＝2,－2　　イ　x＝0,－4 　ウ　x＝0, 4　　　エ　x＝4
５	a人が1人500円ずつ出して,b円の花束を買おうとしたところ,200円たりなかった。このときの数量の関係を表す式として,正しいものを次のア～エから1つ選び,記号を書きなさい。ただし,消費税は考えないものとする。 　ア　500a－200＝b　　イ　500a＞b＋200 　ウ　500a－b＜200　　エ　500a＝b－200	10	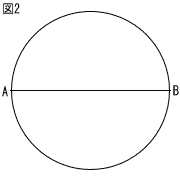図2は,線分ABを直径とする円である。この円を線分ABと直線lの2本で合同な4つの図形に分けるとき,直線lを定規とコンパスを使って作図しなさい。ただし,直線を表す文字l も書き,作図に用いた線は消さないこと。
６	資料は,あるクラスの徒歩通学生徒16名の通学時間を調べ,その値を左から小さい順に並べたものである。通学時間の中央値を求めなさい。 〔資料〕 　5， 8，10，10，12，15，15，15，19， 　20，20，23，25，　27，30，35 　　（単位：分）	11	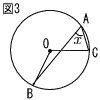図3は,円Oの円周上の3点A,B,Cについて,点AとB,点AとC,点OとB,点OとCを結んだものであり,∠BOC＝ 120°とする。 (1) ∠xの大きさを求めなさい。 (2) OB＝6cmのとき,点Aをふくまないおうぎ形OBCの面積を求めなさい。