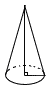| 【 後 期 】 次の1~15の中から,指示された8 問について答えなさい。 |
| 1 |
(1)  4-5×3 4-5×3
(2)  (4-5)×3 (4-5)×3 |
10 |
√306-3n が自然数となるような整数nのうち,最も大きい値を求めなさい。
|
| 2 |
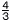 ab2÷2b×(-3a) ab2÷2b×(-3a)
|
11 |
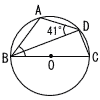 右の図で,4点A,B,C,Dは円Oの周上の点であり,線分BCは円Oの直径である。∠ADB=41°のとき,∠ABC の大きさを求めなさい。 右の図で,4点A,B,C,Dは円Oの周上の点であり,線分BCは円Oの直径である。∠ADB=41°のとき,∠ABC の大きさを求めなさい。
|
| 3 |
|
| 4 |
xについての方程式 2x+a-1=0 の解が3のとき,aの値を求めなさい。
|
12 |
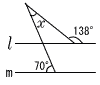 右の図で,2直線l ,mは平行である。このとき,∠xの大きさを求めなさい。 右の図で,2直線l ,mは平行である。このとき,∠xの大きさを求めなさい。 |
| 5 |
x=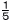 ,y=3のとき,3(x-5y)-2(4x-7y)の値を求めなさい。 ,y=3のとき,3(x-5y)-2(4x-7y)の値を求めなさい。 |
13 |
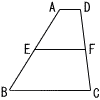 右の図において,四角形ABCDはAD//BCの台形であり,点 E,Fはそれぞれ辺AB,CDの中点である。AD=3㎝,BC=11㎝のとき,線分EFの長さを求めなさい。 右の図において,四角形ABCDはAD//BCの台形であり,点 E,Fはそれぞれ辺AB,CDの中点である。AD=3㎝,BC=11㎝のとき,線分EFの長さを求めなさい。 |
| 6 |
方程式 x2-5x+6=0 を解きなさい。
|
| 7 |
次の表は,xとyの関係を表したものである。yが x
| x |
… |
-1 |
0 |
… |
3 |
… |
| y |
… |
□ |
× |
… |
2 |
… |
に反比例するとき,表の□にあてはまる値を求めなさい。
|
14 |
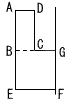 右の図のように,長方形ABCDと正方形BEFGが同じ平面上にあり,点Cは線分BGの中点で,AB=BE=4㎝である。長方形ABCDと正方形BEFGを合わせた図形を,直線GFを軸として1回転させてできる立体の体積を求めなさい。 右の図のように,長方形ABCDと正方形BEFGが同じ平面上にあり,点Cは線分BGの中点で,AB=BE=4㎝である。長方形ABCDと正方形BEFGを合わせた図形を,直線GFを軸として1回転させてできる立体の体積を求めなさい。
ただし,円周率をπとする。
|
| 8 |
サイクリングコースの地点Aから地点Bまで自転車で走った。地点Aを出発して,はじめは時速13kmでakm走り,途中から時速18kmでbkm走ったところで,地点Bに到着し,かかった時間は1時間であった。このときの数量の関係を等式で表しなさい。 |
| 9 |
| 階級(点) |
度数(人) |
| 0 |
3 |
| 1 |
4 |
| 2 |
ア |
| 3 |
イ |
| 4 |
4 |
| 5 |
2 |
| 合計 |
17 |
右の度数分布表は,17人があるゲームを行ったときの得点の記録をまとめたものである。得点の中央値が2点であるとき,ア,イにあてはまる数の組は何組あるか,求めなさい。 |
15 |
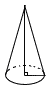  右の図のように,底面の半径が2㎝,表面積が40π㎝2の円錐(すい)がある。この円錐の高さを求めなさい。ただし,円周率をπとする。 右の図のように,底面の半径が2㎝,表面積が40π㎝2の円錐(すい)がある。この円錐の高さを求めなさい。ただし,円周率をπとする。
|
 右の図で,4点A,B,C,Dは円Oの周上の点であり,線分BCは円Oの直径である。∠ADB=41°のとき,∠ABC の大きさを求めなさい。
右の図で,4点A,B,C,Dは円Oの周上の点であり,線分BCは円Oの直径である。∠ADB=41°のとき,∠ABC の大きさを求めなさい。 右の図で,2直線l ,mは平行である。このとき,∠xの大きさを求めなさい。
右の図で,2直線l ,mは平行である。このとき,∠xの大きさを求めなさい。 右の図において,四角形ABCDはAD//BCの台形であり,点 E,Fはそれぞれ辺AB,CDの中点である。AD=3㎝,BC=11㎝のとき,線分EFの長さを求めなさい。
右の図において,四角形ABCDはAD//BCの台形であり,点 E,Fはそれぞれ辺AB,CDの中点である。AD=3㎝,BC=11㎝のとき,線分EFの長さを求めなさい。 右の図のように,長方形ABCDと正方形BEFGが同じ平面上にあり,点Cは線分BGの中点で,AB=BE=4㎝である。長方形ABCDと正方形BEFGを合わせた図形を,直線GFを軸として1回転させてできる立体の体積を求めなさい。
右の図のように,長方形ABCDと正方形BEFGが同じ平面上にあり,点Cは線分BGの中点で,AB=BE=4㎝である。長方形ABCDと正方形BEFGを合わせた図形を,直線GFを軸として1回転させてできる立体の体積を求めなさい。