全国公立高校入試 　１番問題　【平成２９年春】	正　答　６
	41　佐賀県　〜　47　沖縄県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

41佐賀県	１ (1) 4 　(2)   9×(−4) ＝− 12 15  5 　(3) −12＋8x−6x＋9＝2x−3 　(4) 3√5−√5＝2√5 ２ 3a≦100 ３ 2x＋x＝15より，x＝5 ４ (x＋7)(x−4) ５ 解の公式より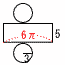， 　x＝ −3±√32−4×2×(−4) 2×2 　x＝ −3±√41 4 ６ �C ７（右図参照） 側面（長方形）の横＝底面の円周 　5×6π＝30πcm2 ８ �B ９ 2つの式に分けて 　{  3x−4y＝17  5x−y＝17  　これを解いて，x＝3，y＝−2	44熊本県	１ 　7×8 ＝14　　２ 10−15＝−5 　4×1 ３ 　5x＋7y＋2(x−4y) ＝ 7x−y  　2 2  ４ −8×a2b2×6b＝−48a2b3 ５ 9x2−(9x2−6x＋1)＝6x−1 ６ √3(√2＋1）×2(√2−1） 　＝2√3(√2＋1）(√2−1） 　＝2√3(2−1)＝2√3 　〜２番問題（おまけ）〜 １ 両辺を10倍して， 　　13x−20＝7x＋10 　　6x＝30より，x＝5 ２ 方程式は，x＋x2＝3 　　　（x2＋x−3＝0も可） 解の公式より， 　x＝ −1±√12−4×1×(−3) 2×1 　x＝ −1±√13 2 ４ △ＢＣＤは直角二等辺三角形 　∠ＤＣＥ＝∠ＡＢＥ＝180−(90＋28＋45) 　　＝180−163＝17°
42長崎県	１ 10−6＝4　　２  　5＋6 ＝ 11 　3×5 15 ３ 2√5＋√5＝3√5 ４ 与式＝(x−y)2＝(2−1)2＝1 ５ 外項の積＝内項の積だから， 　x×4＝16×5で，4x＝80より，x＝20 ６ 上式×2＋下式より， 　7x＝21で，x＝3 　これを上式に代入して， 　　2×3＋y＝8より，y＝2 　よって，x＝3，y＝2 ７ 解の公式より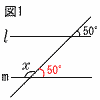， 　x＝ −(−1)±√(−1)2−4×1×(−3) 2×1 　x＝ 1±√13 2 ８ y＝axに，(3,−6）を代入して， 　　−6＝3aより，a＝−2 　よって，y＝−2x ９（右図参照） 　平行線上の錯角は 　　等しいから， 　∠x＝180-50＝130° 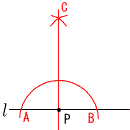10 解は右図 （作図法） ・l 上に，ＰＡ＝ＰＢとなる 　2点Ａ,Ｂをとる ・ＡとＢからＡＣ＝ＢＣ 　となる点Ｃをとる ・ＰとＣを結ぶ	45宮崎県	１ −13　　２ 　−5×8 ＝−  2  　4×15  3 ３ 7＋9＝16 ４ 3a−3b＋2a−4b＝5a−7b ５ √24＝2√6 ６ xの増加量＝4−1＝3 　yの増加量＝(−42)−(−12) 　　＝−16＋1＝−15 　よって，変化の割合＝ −15 ＝−5 3  ７ 出かたは全部で，23＝8通り 　1枚表は次の3通り 　　表裏裏，裏表裏，裏裏表 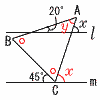　よって，確率＝  3  8 ８（右図参照） 　∠Ａ＝∠yとすると， 　　∠x＝∠y＋20　…ア 　∠ＡＢＣ＝（180−∠y）÷2…イ ア＋イ＋45＝180より， 　（∠y＋20)＋（90−∠y/2)＝135 　∠y/2＝25より，∠y＝50° 　アに代入して，∠x＝50＋20＝70° ９ 弧の長さは中心角に比例するから， 　∠ＡＯＰ＝∠ＰＯＢ＝3：1 　よって，∠ＰＯＢ＝45°になればよい。 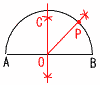解は右図 （作図法） ・線分ＡＢの垂直二等分線 ・∠ＢＯＣの二等分線 ・円周との交点をＰとする
43大分県	１ (1) 3　　(2) 3−9＝−6 　(3) 8a−12−6a＋10＝2a−2 　(4)  　4(x−y)−3(x＋y） ＝ x−7y  　24 24  　(5) 6√2−5√2＋3√2＝4√2 ２ x2−4＝6x−4 　　x(x−6)＝0より，x＝0,6 ３ 走った道のりをxmとすると， 　1800−x ＋  x　 ＝56−30  　60 100 　両辺×300より， 　　5(1800−x)＋3x＝26×300 　　9000−5x＋3x＝7800 　　−2x＝−1200より，x＝600m ４ 下記の理由から，イ  　 A B ア 範　　囲  240分 180分 イ 最頻値の階級 120〜150 150〜180 ウ 中央値の階級 120〜150 120〜150 エ 150分以上 8人 10人 ５ 同時2球の取り出し方は 　　　全部で，6×5÷2＝15通り 　赤球1個は3通り，白球1個も3通り 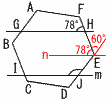　よって，確率＝ 3×3 ＝  3 15   5 ６（右図参照） ・l,mに平行線nを引く 　同位角から78° 　外角から60° 　∠ＩＪＥ＝78+60＝138° ７ 解は右図 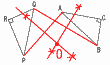（作図法） ・線分ＡＰの垂直二等分線 ・線分ＢＰの垂直二等分線 ・2本の垂直二等分線の 　　交点を中心Ｏとする （線分ＣＲの垂直二等分線でもよい）	46鹿児島県	１ (1) 83−5＝78 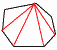　(2)　  2×5 ＋  3 ＝ 2＋3 ＝  5 10×8 16 16 16 　（3) −16＋9＝−7　　(4) ±√6 　(5) 5つの三角形に分割できるから， 　　　180×5＝900° ２ アは，y＝60x （比例） 　　イは，y＝1000−120x （1次関数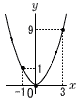） 　よってウで，y＝ 36 x ３ y＝−5(x−2)＋1より， 　　y＝−5x＋11 ４（右上図参照） 　x＝−1のとき，y＝(−1)2＝1 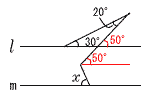　x＝0のとき，y＝02＝0 　x＝3のとき，y＝32＝9 　よって，0≦y≦9 ５（右図参照） 　20＋30＝50° 　∠x＝115−50＝65°
		47沖縄県	１ 2−10＝−8　　２ 　　1×2  ＝−  2  5×(−3) 15 ３ 12.96　　４ 3√2＋2√2＝5√2 ５ 9x2　　６ 3x＋2−x＋4＝2x＋6 　〜２番問題（おまけ）〜 １ −y＝−3x−6で，y＝3x＋6 ２ 上式＋下式より， 　　　3x＝6で，x＝2 　　これを上式に代入して， 　　　2×2＋y＝5で，y＝5−4＝1 　よって，x＝2，y＝1 ３ 与式＝x2−4 ４ 与式＝a(a−8) ５ 解の公式より， 　x＝ −5±√52−4×1×1 ＝ −5±√21 2×1 2 ６ √64＝8

［トップに戻る］　［前ページに戻る］