| １ |
(1)  3−12
|
４ |
大小2つのさいころを同時に1回投げ，大きいさいころの出る目の数を十の位の数，小さいさいころの出る目の数を一の位の数として，2けたの整数をつくる。
このとき，つくられる2けたの整数が8の倍数となる確率を求めなさい。
ただし，大小2つのさいころのそれぞれについて，1から6までのどの目が出ることも，同様に確からしいものとする。
|
(2) 2×(−3)2−22
|
(3) 3(2a−3b)−(a−5b)
|
５ |
 下の資料は，ある中学校の生徒11人の1か月間に読んだ本の冊数を示したものであり，中央値（メジアン）と平均値が等しい。
資料の［a］に適する数を求めなさい。ただし，［a］に適する数は自然数とする。
読んだ本の冊数（冊）
|
(4) x4y3÷x2y2×x2y
|
(5) √20＋2√5−√45
|
６ |
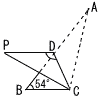 右の図のように，∠ＡＢＣ＝54°である△ＡＢＣの辺ＡＢ上に点Ｄをとり，線分ＣＤを折り目として△ＡＢＣを折り返し，頂点Ａが移った点をＰとする。
ＰＤ//ＢＣのとき，∠ＰＤＣの大きさを求めなさい。
|
| ２ |
次の連立方程式を解きなさい。
|
７ |
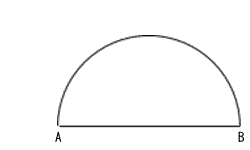
下の図のように，線分ＡＢを直径とする半円がある。弧ＡＢ上に点Ｐをとり，∠ＰＡＢ＝15°となる線分ＡＰを作図しなさい。
ただし，作図には定規とコンパスを用い，作図に使った線は消さないこと。
|
| ３ |
2次方程式 (x＋1)(x−6)＋9＝0 を解きなさい。
|
