全国公立高校入試 　１番問題　【平成２７年春】

（３）秋田県

学習日　　　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１	(1)　　−3×(5−7) (2)　　−3−5×2	８	yはxに反比例し，x＝4のとき，y＝−12である。　このとき，yをxの式で表しなさい。
２	方程式  4x＋5 ＝x　を解きなさい。  3	９	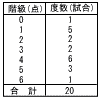右の度数分布表は，あるサッカーチームが行った試合の得点の記録をまとめたものである。　この表から試合の得点の最頻値と平均値をそれぞれ求めなさい。
３	(√7＋1)(√7−2)
４	連立方程式｛ 9x−2y＝25･･･�@ を解き 2x−y＝10　･･･�A なさい。 計算の過程も書きなさい。	10	√3aが１けたの自然数になるような自然数aの値をすべて求めなさい。
		11	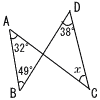右の図で，∠ＡＢＤ＝49°，∠ＢＡＣ＝32°，∠BDC＝38°である。　このとき，∠xの大きさを求めなさい。
５	方程式　x2＋ax＋8＝0　の解の1つが4のとき，aの値を求めなさい。　また，もう1つの解も求めなさい。　 計算の過程も書きなさい。	12	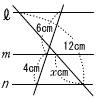右の図で，３直線 l ，m，nは，いずれも平行である。　このとき，xの値を求めなさい。
		13	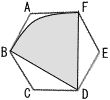右の図で，六角形ＡＢＣＤＥＦは，1辺の長さが2cmの正六角形である。　この六角形の対角線DBを半径とし，∠BDFを中心とするおうぎ形DBFの面積を求めなさい。　ただし，円周率をπとする。
６	1本a円の鉛筆3本と，b円の筆箱1個を買ったとき，代金の合計が700円より高くなった。　この数量の関係を不等式で表しなさい。	14	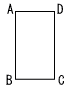右の図で，四角形ABCDは，AB＝7cm，BC＝4cmの長方形である。　この長方形を辺ABを軸として１回転させてできる立体の表面積を求めなさい。　ただし，円周率をπとする。
７	x＝  4 ，y＝−2のとき，3(４x−y)−(2x−5y)  5 の値を求めなさい。	15	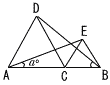右の図で，点Cは線分AB上の点であり，△DACと△ECBは，それぞれ線分ACと線分CBを１辺とする正三角形である。　∠EAC＝a°とするとき，∠ＤＢＣの大きさをaを用いた式で表しなさい。