| 【 前 期 】 （７は省略） |
【 後 期 】 （５は省略） |
| １ |
(1)  −7＋4
(2) 0.2÷(−5)
(3) 13−(−2)3×7
(4) (4x−y)−2(x−5y)
|
１ |
(1) 5−6
| (2) |
7 |
÷(− |
7 |
) |
| 6 |
2 |
(3) 2−52×(−3)
(4) 28a2b÷7ab×(−3b)
|
| ２ |
次の連立方程式を解きなさい。
|
２ |
x＝−1,y＝5のとき，次の式の値を求めなさい。
−2(x−5y)＋(4x−3y)
|
| ３ |
132を素因数分解しなさい。
|
３ |
次の式を因数分解しなさい。
x2−9x−36
|
| ４ |
次の二次方程式を解きなさい。
x2＋7x＋2＝0
|
４ |
次の二次方程式を解きなさい。
x2−5x＋3＝0
|
| ５ |
yはxに比例し，x＝5，y＝3である。x＝−35のときのyの値を求めなさい。
|
６ |
ある工場で作った製品の中から無作為に250個取り出して調べると，3個が不良品であった。この工場で作った20000個の製品の中には，およそ何個の不良品があると考えられるか，求めなさい。
|
| ６ |
あるセーターを，ゆきさんは定価の35%引きで，あきさんは定価の500円引きで買ったところ，ゆきさんはあきさんより270円安く買うことができた。このセーターの定価を求めなさい。
|
７ |
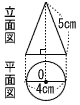 右の投影図で表される立体の表面積を求めなさい。 ただし，平面図の図形は円Oである。
|
| ８ |
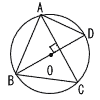  右の図のように，円Oの円周上に4点A,B,C,Dをとる。∠ABC＝66°のとき，∠ADBの大きさを求めなさい。
|
８ |
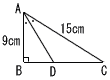 右の図の△ABCで，AB＝9cm,AC＝ 15cm,∠B＝90°である。∠Aの二等分線とBCとの交点をDとするとき，CDの長さを求めなさい。
|
