全国公立高校入試 　１番問題　【平成２４年春】	正　答　６
	41佐賀県　〜　47沖縄県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

41佐賀県	１　ア　−3 　　イ . 　1×15 . ＝− 3 5×(−4) 4 　　ウ　−2ａ＋4ｂ＋3ｂ−12ａ＝−14ａ＋7ｂ 　　エ　5−4＝1 ２　下式を上式に代入して， 　　　　ｘ＋2(3ｘ−5)＝4 　　　　　ｘ＋6ｘ−10＝4 　　　　　　　　　　７ｘ＝14で，ｘ＝2 　　これを下式に代入して， 　　　　ｙ＝3×2−5＝1 　　よって，ｘ＝2，ｙ＝1 ３　解の公式より， 　　ｘ＝ −(−5)±√(−5)2−4×2×1 　　　　　　　　2×2　　　　　　　 　　　＝ 5±√25−8 ＝ 5±√17 　　　　4　　　 　　4　　 ４　表裏の出方は全部で，23＝８通り 　　このうち２枚表は，３通り 　よって求める確率は， ３ ８ ５　円柱 ６　ア　ＡＢが直径だから，∠ＡＣＢ＝90° 　　　　∠ＢＡＣ＝180−90−30＝60° 　　　　∠ｘ＝∠ＢＡＣ＝60° 　　イ　△ＡＢＣで， 　　　　　　ＡＢ：ＢＣ＝2：√3だから， 　　　　　　　2：ＢＣ＝2：√3 　　　　よって，ＢＣ＝√3cm	45宮崎県	１　−9＋2＝−7 ２　− 2×9 ＝− 3 3×4 2 ３　−2ａ−2ｂ＋3ａ−2ｂ＝ａ−4ｂ ４　√25−√9＝5−3＝2 ５　解の公式より， 　ｘ＝ −5±√52−4×3×1 　　　　　　2×3　　　　 　　＝ −5±√125−25 ＝ −5±√13 　　　　　6　　　　 　　　6　　　 ６　. 　4 . ＝ 　 ｘ　. 200 50000 　　200ｘ＝200000 　　　　 ｘ＝1000個 ７　ｘ＝1のとき，ｙ＝3×12＝3 　　ｘ＝4のとき，ｙ＝3×42＝48 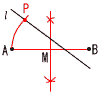　よって，変化の割合＝ 48−3 ＝15 　4−1 ８　線分ＡＢを直径とする 　　　　　　　円をかけばよい。 　(1)　ＡＢの垂直二等分線を引く 　(2)　ＡＢの中点Ｍをとる 　(3)　ＭＡ＝ＭＰとなる弧をかく 　(4)　弧ととの交点をＰとする
42長崎県	１　7−12＝−5 ２　. 3×5−2×4 ＝ ７ 　　4×5　　 20 ３　3√7−2√7＝√7 ４　2ｘ3ｙ ５　結果を小さい順に並べると， 　　　　　23，28，28，35，38，39，40，41 　　８人の中央値だから， 　　　　　4人目と５人目の平均値をとればよい。 　　(35＋38)÷2＝36.5分 ６　　上式×2　　6ｘ＋2ｙ＝20 　　　下式　　 ＋）ｘ−2ｙ＝1 　　　　　　　　　　7ｘ　　 ＝21 　　　　　　　　　　　　　ｘ＝3 　　　これを上式に代入して， 　　　　　3×3＋ｙ＝10 　　　　　　　　　ｙ＝10−9＝1 　　　よって，ｘ＝3，ｙ＝1 ７　解の公式より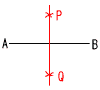， 　ｘ＝ −(−5)±√(−5)2−4×1×3 　　　　　　　　2×1　　　　　　　 　　＝ 5±√25−12 ＝ 5±√13 　　　　2　　　 　　2　　 ８　∠ｘ＋40＝50＋20 　　∠ｘ＝70−40＝30° ９　. 4 π×33＝36πcm3 3 10　（右図参照） 　　ＡＰ＝ＢＰとなる点をとる 　　ＡＱ＝ＢＱとなる点をとる 　　点Ｐと点Ｑを結ぶ	46鹿児島県	１　(1)　8＋28＝36 　 (2) . 3×10 − 2 ＝ 1×2 − 2 5×9 5 1×3 5 　　　　＝ 10−6 ＝ 4 　15　 15 　 (3) . 6ｘ3ｙ×4ｙ2 ＝8ｘ2ｙ 　　3ｘｙ2　 　　(4)　両辺を9倍して，9ｃ＝10ａ−ｂ 　　　　　移項して，ｂ＝10ａ−9ｃ 　　(5)　与式＝(9−2)＋(3−2√2)＝10−2√2 　　　　　　　＝10−2×1.4＝10−2.8＝7.2 ２　(ｘ−5)(ｘ＋3) ３　6000×(1−0.4)×(1−0.1)＝6000×0.6×0.9 　　＝3600×0.9＝3240円 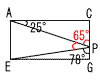４　平均値＝ 62×5＋66×6＋70×1 　　　　　　　12　　　　　　 　　　　　　＝ 310＋396＋70 ＝ 776 ≒64.7ｍ 　　　　12　　　 12 ５　（右図参照） 　△ＡＰＣで， 　　　∠ＡＰＣ＝90−25＝65° 　よって， 　　　∠ＡＰＥ＝180−65−78 　　　　　　　　＝37°
43大分県	１　(1)　−5　　　(2)　6−4＝2 　　(3)　6ａ−3ｂ＋2ａ−4ｂ＝8ａ−7ｂ 　 (4) . ｘｙ2×4ｘ2 ＝2ｙ 　2ｘ3ｙ　 　　(5)　2√6＋4√6−3√6＝3√6 ２　ｘ2＋ｘ−6＝−3 　　ｘ2＋ｘ−3＝0 　　解の公式より， 　　　ｘ＝ −1±√12−4×1×(−3) 　　　　　　　　2×1　　　　　　 　　　　＝ −1±√1＋12 ＝ −1±√13 　　　　　2　　　　 　　　2　　　 ３　ｘ＝−2を元の方程式に代入して， 　　　　−2ａ−3(ａ−2)×(−2)＝8−4×(−2) 　　　　−2ａ＋6(ａ−2)＝8＋8 　　　　4ａ＝16＋12より，ａ＝7 ４　両辺を3倍すると，3ａ＝ｂ−2ｃ 　　移項して，2ｃ＝ｂ−3ａ 　　よって，ｃ＝ ｂ−3ａ 　または，ｃ＝ −3ａ＋ｂ 　　2　 　　2　　 ５　２けたの整数は全部で，4×3＝12通り， 　　３の倍数は，12，21，24，42の4通りできる。 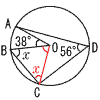　よって， 4 ＝ 1 12 3 ６　∠ＡＯＣ＝56×2＝112° 　　　　　　　　　　　　　　　(中心角) 　　∠ＢＯＣ＝112−38＝74° 　　△ＯＢＣで， 　　　　∠ｘ＝(180−74)÷2＝53° 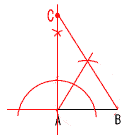７　（右図参照） (1)　線分ＢＡを左に延長する (2)　Ａから垂線を上側に作図 (3)　ＡＢを１辺とする正三角形 　　を作図 (4)　Ｂから延長し， 　　　　垂線との交点Ｃをとる	47沖縄県	１　−3 ２　. 8＋3 ＝ 11 　12　 12 ３　　　 0.72 　　　6）4.32 　　　　 42 . 　　　　　 12 　　　 　　12 　　　　　　 0 ４　9＋10＝19 ５　3√5−2√5＝√5 ６　3ｘ−6ｙ−8ｘ＋6ｙ＝−5ｘ 　〜　２番問題の一部　（おまけ）　〜 ２　9ｘ−4ｘ＝17−2 　　　　　5ｘ＝15 　　　　　　ｘ＝3 ３　(2ｘ)2−2×2ｘ＋12＝4ｘ2-4ｘ＋1 ４　(ｘ−1)(ｘ−6) ５　　　　 　　4ｘ−2ｙ＝14 　　　　　＋）3ｘ＋2ｙ＝ 7 　　　　　　　 7ｘ　　 ＝21 　　　　　　　　　　　ｘ＝3 　　よって，ｘ＝3，ｙ＝−1 ６　解の公式より， ｘ＝ −5±√52−4×2×1 ＝ −5±√25−8 　　　　　　2×2　　　　 　　　　4　　　　 　＝ −5±√17 　　　4　　　 ７　. √2×√5 ＝ √10 √5×√5 　5
44熊本県	１　16　　　　２　−8＋6＝−2 ３　9ｘ−13＋28−7ｘ＝2ｘ＋15 ４　3ａ−2ｂ ５ . 5(3ｘ−ｙ)−2(7ｘ−ｙ) ＝ 15ｘ−5ｙ−14ｘ＋2ｙ 　　　　　　10　　　　　 　　　　　　10　　　　　 　　　＝ ｘ−3ｙ 　10　 ６　2＋2√2＋1−√2＝3＋√2 　〜　２番問題の一部　（おまけ）　〜 １　2ｘ＋4ｘ＝17−5 　　6ｘ＝12より，ｘ＝2 ２　ｘ2−ｘ−1＝0 　　解の公式より， 　　　ｘ＝ −(−1)±√(−1)2−4×1×(−1) 　　　　　　　　　　2×1　　　　　　　　　 　　　　＝ 1±√1＋4 ＝ 1±√5 　　　2　　　 　　2　 ３　2√3＋√［ア］＝√［イ］ 　　たし算するには，根号内が同じ数。 　　　　よって，ア＝3 　　2√3＋√3＝3√3＝√27 　　　　よって，イ＝27