全国公立高校入試 　１番問題　【平成２４年春】

（２５）　滋賀県

学習日　　　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１	(1)　6÷2−5 　　　　　　　　　　　　　　　　　　　　　　　　　 . (2)　2(4ａ−3)−6ａ 　　　　　　　　　　　　　　　　　　　　　　　　　 . (3)　8ｘ2ｙ×2ｙ÷(−4ｘ)2 　　　　　　　　　　　　　　　　　　　　　　　　　 . (4)　(ｘ＋4)2−(ｘ＋7) 　　　　　　　　　　　　　　　　　　　　　　　　　 . (5) . √12 − 　2 . 　6　 √3 　　　　　　　　　　　　　　　　　　　　　　　　　 .	４	図１のように，半径１の円Ｏの円周を６等分する点Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆがある。次の(1)，(2)の問いに答えなさい。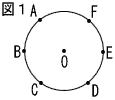 (1)　さいころの６つの面に，図１の円周上の点を表すＡからＦの文字のシールがはってある。このさいころを２回投げ，出た文字の２つの点を結んだとき，線分の長さが１になる確率を求めなさい。ただし，同じ文字が出たときは線分の長さを０とする。また，どの文字が出ることも同様に確からしいとする。 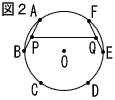　　　　　　　　　　　　　　　　　　　　　　 . (2)　図２のように，線分ＡＢ，ＥＦの中点を，それぞれＰ，Ｑとするとき，線分ＰＱの長さを求めなさい。 　　　　　　　　　　　　　　　　　　　　　　 .
２	次の２次方程式を解きなさい。 　　　ｘ2＋4ｘ−9＝−ｘ＋5 　　　　　　　　　　　　　　　　　　　　　　　　　 .	５	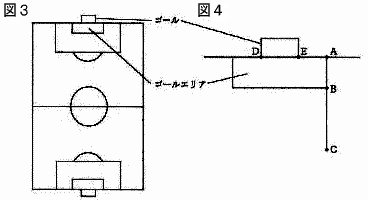図３のサッカー場のゴール付近で，シュートを打つ練習をする。図４のように，ゴールエリアの長方形の辺ＡＢを延長し，ＡＣ＝3ＡＢとなる点をＣ，ゴールライン上のゴールポストの位置を示す点をＤ，Ｅとする。線分ＡＣ上の２点Ｃ，Ｐからゴールに向かってシュートを打つとき，∠ＤＣＥ＝∠ＤＰＥとなる点Ｐをコンパスと定規を使って作図しなさい。ただし，作図に使った線は消さないこと。
３	ｙ はｘ の２乗に比例し，ｘ＝2のとき，ｙ＝−8となる。ｘ＝6のとき，ｙ の値を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい