全国公立高校入試
　１番問題　【平成２４年春】
（１１）　埼玉県 　学習日　　　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１ 　8ｙ−2ｙ

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　		 ９ 　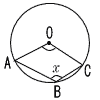右の図のように，点Ｏを中心とする円の周上に３点Ａ，Ｂ，Ｃをとり，四角形ＯＡＢＣをつくります。∠ＡＯＣと∠ＡＢＣの大きさが等しいとき，∠ＡＢＣの大きさｘ を求めなさい。



　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　
２ 　4×(−3)＋7

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　
３ 　√27−√3

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　		 10 　Ｓさんは，近くに完成した高さ634ｍの新タワーまでの距離を，高さ12.5ｍの電柱を目印にして求めようと考えました。Ｓさんは，電柱の先端と新タワーの先端が一致して見える位置に立ち，その位置から電柱までの距離を測ったら，ちょうど10ｍでした。
　このとき，Ｓさんが立っている位置から新タワーまでの距離は何ｍかを求めなさい。
　ただし，Ｓさんの目の高さを1.5ｍとします。また，Ｓさん，電柱，新タワーは，同じ平面上に垂直にたっており，それぞれの幅や厚みは考えないものとします。


　　　　　　　　　　　　　　　　　　　　　　　　　 .
　
４ 　ｘ＝16のとき，ｘ2−3ｘ−28　の値を求めなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　
５ 　２次方程式　2ｘ2−5ｘ＋1＝0　を解きなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　
６
　連立方程式　｛ . ｘ＋2ｙ＝5 を解きなさい。
2ｘ−3ｙ＝3



　　　　　　　　　　　　　　　　　　　　　　　　　 .
　		 11 　次は，Ｔさんが所属している柔道部の男子部員12人全員が，鉄棒で懸垂をした回数の記録です。下のア，イに答えなさい。

件数の回数の記録（回）
　6，5，8，3，3，4，5，24，28，3，7，6　.

ア
　平均値と中央値（メジアン）をそれぞれ求めなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　 .

イ
　Ｔさんの懸垂の回数は８回でした。家に帰ると，兄にＴさん自身の懸垂の回数と，柔道部員の平均値を聞かれました。それに答えると「平均値と比べると，柔道部の男子の中では懸垂ができない方だね。」と言われました。この兄の意見に対する反論とその理由を述べ，代表値として平均値よりふさわしいものを書きなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　 .
　
７
　関数　ｙ＝− 1 ｘ2　で，ｘ の変域が
2
−2≦ｘ≦1のとき，ｙの変域を求めなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　 .
　
８ 　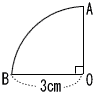右の図のような，半径3cmで中心角が90°のおうぎ形ＯＡＢがあります。このおうぎ形ＯＡＢを，線分ＡＯを軸として１回転させてできる立体の体積を求めなさい。
　ただし，円周率はπとします。


　　　　　　　　　　　　　　　　　　　　　　　　　 .
　

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい