全国公立高校入試 　１番問題　【平成２３年春】	正　答　６
	４１　佐賀県　〜　４７　沖縄県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

41佐賀県	［前期］ １　8＋6＝14 ２　2−2√2−3＝−1−2√2 ３　両辺×4より，ｘ−1＝8ｘ−12 　　　　−7ｘ＝−11で，ｘ＝11/7 ４　解の公式より， 　　　ｘ＝ −(−7)±√｛(−7)2−4×2×4｝ 　　　　　　　　　2×2　　　　　　　　 　　　　＝ 7±√(49−32) ＝ 7±√17 　　　　　4　　　 　　4　　 ５　ｘ＝3のとき，ｙ＝−2×32＝−18 　　ｘ＝−1のとき，ｙ＝−2×(−1)2＝−2 　　ｘ＝0のとき，ｙ＝−2×02＝0 　　　　よって，−18≦ｙ≦0 ６　(ア)　5×4÷2＝10通り 　　(イ)　両方とも奇数となるのは， 　　　　　　　1と3，1と5，3と5　の３通り 　　　　　少なくとも一方が偶数となるのは， 　　　　　　　10−3＝７通り 　　　　　よって，求める確率は，7/10 　［後期］ １　(ア)　3 　 (イ)　. 4ａ×6ｂ ＝−8 −3ａｂ 　 (ウ)　4＋4√3＋3＝7＋4√3 ２　(4ｘ＋3)(4ｘ−3) ３　(ｘ−3)(ｘ＋2)＝0より，ｘ＝3，−2 ４　ｙ＝ ａ に，ｘ＝2，ｙ＝−10を代入して， ｘ 　−10＝ ａ で，ａ＝−20 2 　よって，ｙ＝− 20 に，ｘ＝4を代入して， ｘ 　　　　　ｙ＝− 20 ＝−5 4 ５　 　２回とも白玉の確率は，( 2 )2＝ 4 5 25 　２回とも黒玉の確率は，( 3 )2＝ 9 5 25 　　よって， 4 ＋ 9 ＝ 13 25 25 25 ６　(ア)　∠ＡＣＢ＝180−45−90＝45° 　　　　△ＡＢＣは二等辺三角形だから， 　　　　　　ＢＣ＝ＡＢ＝4ｃｍ 　　(イ)　ＢＥ＝√(62−42)＝√(36−16) 　　　　　　　 ＝√20＝2√5ｃｍ 　　　　よって，1/2×42×2√5＝16√5ｃｍ3	44熊本県	１　6.3 ２　1−2＝−1 ３　. 9ａ−5−2ａ＋8 ＝ 7ａ＋3 　　　　　2　　　 　　2　 ４　. 6ｘ×4ｙ2 . ＝3ｘｙ 　　　8ｙ　 ５　9ａ2−6ａｂ＋ｂ2＋7ａ2＋6ａｂ−ｂ2＝16ａ2 ６　√2(√5−√3)(√5＋√3)＝√2(5−3) 　　＝2√2 　〜　２番問題　（おまけ）　〜 １　2ｘ＝6より，ｘ＝3 ２　2(ｘ2＋3ｘ−10)＝2(ｘ＋5)(ｘ−2) ３　ｙ＝ ａ とすると，Ａ(3， ａ )，Ｂ(−1，−ａ) ｘ 3 　　よって， ａ −(−ａ)＝8 3 　　これを解いて， 4 ａ＝8より，ａ＝6 3 　　よって，ｙ＝ 6 ｘ ４　ａ(ａ−１)＝28より， 　ａ . 1 2 4 7 14 28 ｂ−1 28 14 7 4 2 1 　　また，2＜√ａ＜3より，２乗して， 　　　　　4＜ａ＜9 　　上の表の中では，ａ＝7 　　　　このときｂ−1＝4より，ｂ＝5 　　よって，ａ＝7，ｂ＝5
42長崎県	［　Ａ　］ １　6−16＝−10 ２　. 6＋1 ＝ 7 　10 10 ３　3√3−2√3＝√3 ４　. 6ｘ2ｙ×ｙ2 . ＝3ｘ2ｙ3 　　　2　　　 ５　2×32＋(−1)3＝18−1＝17 ６　上式×2−下式より， 　　　　3ｙ＝9で，ｙ＝3 　　これを下式に代入して， 　　　　2ｘ＋3＝−1 　　　　2ｘ＝−4で，ｘ＝−2 　　よって，ｘ＝−2，ｙ＝3 ７　解の公式より， 　　　ｘ＝ −3±√(32−4×1×1) 　　　　　　　2×1　　　　　 　　　　＝ −3±√(9−4) ＝ −3±√5 　　　　2　　　　 　　　2　　 ８　ｙ＝ａｘに　(2，6)を代入して， 　　　　6＝2ａで，ａ＝3 　　よって，ｙ＝3ｘ ９　∠ｘ＝31×2＝62° 10　12：22＝1：4＝5：ｘより， 　　　　ｘ＝4×5＝20 　　よって，20ｃｍ2 　［　Ｂ　］ １　1＋2√2＋2− 　4√2 √2√2 　　　　＝3＋2√2−2√2＝3 ２　 ａ3ｂ×(−27ａ3) . ＝−27ａ4 　　　　ａ2ｂ　　　 ３　上式×6より， 　　　　3ｘ＋3ｙ−2ｘ＝6 　　　　　　　　ｘ＋3ｙ＝6 　　これから下式を引いて，ｙ＝4 　　これを下式に代入して， 　　　　ｘ＋2×4＝2で，ｘ＝−6 　　よって，ｘ＝−6，ｙ＝4 ４　ｘ2−1−5ｘ＋ｘ2＝0 　　　　2ｘ2−5ｘ−1＝0 　　解の公式より， 　　ｘ＝ −(−5)±√｛(−5)2−4×2×(−1)｝ 　　　　　　　　　　　　2×2　　　　　　　 　　　＝ 5±√(25＋8) ＝ 5±√33 　　　　4　　　 　　4　　 ５　22：32＝4：9＝8：ｘより， 　　　　4ｘ＝72で，ｘ＝18 　　よって，18ｃｍ2 ６　変化の割合＝ 32ａ−12ａ ＝12 　　3−1　 　　　　. 9ａ−ａ ＝12 　　2　 　　よって，8ａ＝24で，ａ＝3 ７　与式＝ 6√15 　√ｎ 　　よって，ｎ＝15 ８　∠ＡＯＢ＝28×2＝56° 　　∠ｘ＝(180−56)÷2＝62°	45宮崎県	１　−3 ２　. 24×155 ＝ 5 13×82 2 ３　8ａ＋2ｂ−9ａ＋3ｂ＝−ａ＋5ｂ ４　(√12−1)(√12＋1)＝12−1＝11 ５　下式を上式に代入すると， 　　3ｘ−2(3ｘ＋9)＝−6 　　3ｘ−6ｘ＝−6＋18 　　　 −3ｘ＝12より，ｘ＝−4 　　これを下式に代入して， 　　　　ｙ＝3×(−4)＋9＝−3 　　よって，ｘ＝−4，ｙ＝−3 ６　ｘ2−4ｘ−32＝0 　　(ｘ−8)(ｘ＋4)＝0 　　　ｘ＝8，−4 ７　外角の和は３６０°だから， 　　　　３６０÷5＝72° 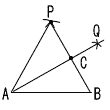８　（右図参照） 　ア　ＡＢを１辺とする正三角形ＰＡＢをかく 　イ　∠ＰＡＢの二等分線ＡＱをかく 　ウ　ＰＢとＡＱの交点をＣとする
		46鹿児島県	１　(1)　72−5＝67 　　(2)　. 9 − 1×8 ＝ 9−4 ＝ 5 14 4×7 　14 14 　　(3)　与式＝8ｘ＋40−12ｘ＋42＝−4ｘ＋82 　　　　　　＝(−4)×(−2)＋82＝90 　 (4)　. 4ａｂ×3ａ2ｂ ＝3ａｂ2 　　　4ａ2　 　 (5)　√18＋ 10√2 √2√2 　　　　＝3√2＋5√2＝8√2 ２　 26000 ＝ 26 ＝ 13 ＝1.857・・・ 14000 14 7 　　小数第２位を四捨五入して，１.９倍 ３　ｙ＝ａｘに，(−3，6)を代入すると， 　　　　6＝−3ａで，ａ＝−2 　　ｙ＝−2ｘに，ｘ＝9を代入して， 　　　　ｙ＝−2×9＝−18 ４　（解答例）　１つ答えればよい 　ｐ＝1の場合， 　　　(2ｘ＋1)(ｘ−5)＝2ｘ2−9ｘ−5 　ｐ＝2の場合， 　　　(2ｘ＋2)(ｘ−5)＝2ｘ2−8ｘ−10 　ｐ＝0の場合， 　　　(2ｘ＋0)(ｘ−5)＝2ｘ2−10ｘ 　ｐ＝−1の場合， 　　　(2ｘ−1)(ｘ−5)＝2ｘ2−11ｘ＋5 ５　ＥＢ＝ＥＣより，∠ＥＢＣ＝∠ＥＣＢ＝58° 　　∠Ｄ＋∠ＢＣＤ＝180°だから， 　　　　(∠ｘ＋58)＋75＝180 　　よって，∠ｘ＝180−58−75＝47°
43大分県	１　(1)　−5 　　(2)　2×9＝18 　　(3)　3ｘ−2−2ｘ＋6＝ｘ＋4 　 (4)　√6− √2√3 ＝√6− √6 ＝ 2 √6 √3√3 　3 3 　 (5)　. 6ａｂ2×9ｂ2 . ＝−18ｂ 　　−3ａｂ3　 ２　鉛筆をｘ本とすると， 　　　生徒の人数から， ｘ−5 ＝ ｘ＋3 　6　 　7　 　　　　　７ｘ−35＝6ｘ＋18 　　　　　　　　　ｘ＝53 　　　よって，５３本 ３　解の公式より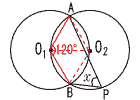， 　　ｘ＝ −(−2)±√｛(−2)2−4×1×(−1)｝ 　　　　　　　　　　2×1　　　　　　　　　 　　　＝ 2±√(4＋4) ＝ 2±2√2 　　　　2　　　 　　2　　 　　　＝1±√2 ４　（右図参照） 　　△ＡＯ1Ｏ2，△ＢＯ1Ｏ2は 　　　　正三角形だから， 　　∠ＡＯ1Ｂ＝60＋60＝120° 　　四角形ＡＯ1ＢＰは 　　　　円Ｏ2に内接するから， 　　∠ｘ＝180−120＝60° ５　与式＝5√2×√(40−ｎ) 　　　　よって，40−ｎ＝2，8，18，32 　　　　　　　　　　　　ｎ＝38，32，12，8 　　このうち最小のものは，ｎ＝8 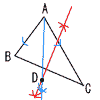６　（右図参照） 　　ア　辺ＢＣの垂直二等分線を引く 　　　　　　　　　　　　　　　（赤線） 　　イ　∠ＢＡＣの二等分線を引く 　　　　　　　　　　　　　　　（青線） 　　ウ　２直線の交点をＤとする	47沖縄県	１　15÷(−3)＝−5 ２　. 7−6 ＝ 1 　3　 3 ３　27÷6＝4.5 ４　ａ3×9ａ2＝9ａ5 ５　4ｘ−2−3ｘ−3＝ｘ−5 ６　2√7＋√7＝3√7 　〜　２番問題　（おまけ）　〜 １　7ｘ−5ｘ＝6＋4 　　　　　2ｘ＝10より，ｘ＝5 ２　9ｘ2＋6ｘ＋1 ３　(ｘ＋3)(ｘ−2) ４　上式×3　　　15ｘ＋6ｙ＝9 　　下式×2　−） 4ｘ＋6ｙ＝20 　　　　　　　　　　 11ｘ　　　＝−11 　　　　　　　　　　　　　　　ｘ＝−1 　　これを下式に代入して， 　　　　2×(−1)＋3ｙ＝10 　　　　　　　　　　　3ｙ＝10＋2で，ｙ＝4 　　よって，ｘ＝−1，ｙ＝4 ５　10ａ＋ｂ ６　5ｙ＝−2ｘ＋3 　　よって，ｙ＝ −2ｘ＋3 　　　5 ７　√9(3)＜√10＜√16(4)だから， 　　　　√10に近いのは，３ ８　ｘ−4＝±√6より，ｘ＝4±√6 ９　与式＝3ｘ−6ｙ−2ｘ＋5ｙ＝ｘ−ｙ 　　　　　＝(−2)−3＝−5 10　90× 43 ＝ 387 ＝38 7 ＝38 42 100 10 10 60 　　よって，38分42秒