全国公立高校入試 　１番問題　【平成２２年春】

（１３）　東京都

学習日　 　　 　　月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１	9＋6÷(− １ ) ３ 　　　　　　　　　　　　　　　　　　　　　　　　　 .	７	１から６までの目の出る大小１つずつのさいころを同時に１回投げる。 　大きいさいころの出た目の数をａ，小さいさいころの出た目の数をｂとするとき，ｂがａの倍数となる目の出方は全部で何通りあるか。 　　　　　　　　　　　　　　　　　　　　　　　　　.
２	ａ−8ｂ−2(ａ−7ｂ) 　　　　　　　　　　　　　　　　　　　　　　　　　 . .
３	(√5＋4)(√5−1) 　　　　　　　　　　　　　　　　　　　　　　　　　 .	８	右の図１のように，２点Ｃ，Ｄは，線分ＡＢを直径とする半円Ｏの弧ＡＢ上にある点で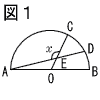， 　弧ＣＤ＝弧ＢＤ＝ １ 弧ＡＢ　である。 ６ 　線分ＡＤと線分ＯＣとの交点をＥとする。 　ｘで示した∠ＡＥＣの大きさは何度か。 　　　　　　　　　　　　　　　　　　　.
４	一次方程式　ｘ＋6＝3ｘ−8　を解け。 　　　　　　　　　　　　　　　　　　　　　　　　　.
５	連立方程式　｛　 4ｘ＋ｙ＝9 　を解け。 ｘ＋5ｙ＝7 　　　　　　　　　　　　　　　　　　　　　　　　　 .	９	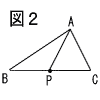右の図２で，点Ｐは△ＡＢＣの辺ＢＣ上にある点で，ＡＰ＝ＢＰである。 　解答欄に示した図をもとにして，線分ＡＰを定規とコンパスを用いて作図し，点Ｐの位置を示す文字Ｐも書け。 　ただし，作図に用いた線は消さないでおくこと。
６	二次方程式　(ｘ＋2)2＝36　を解け。 　　　　　　　　　　　　　　　　　　　　　　　　　 .