|
惓丂摎丂俇丂 | |||
| 41丂嵅夑導丂乣丂47丂壂撽導 |
|
惓丂摎丂俇丂 | |||
| 41丂嵅夑導丂乣丂47丂壂撽導 |
| 41嵅夑導 | 侾丂(1)丂亅5亅2亖亅7 丂丂(2)丂5倶亅3 丂丂(3)丂5併3亅3併3亖2併3 俀丂(倶亄7)(倶亅4) 俁丂斾椺掕悢偑亅1/2偱丆 丂丂丂愨懳抣偑嵟彫偺晧偺悢偩偐傜丆 丂丂壓偵堦斣戝偒偔奐偄偰偄傞僌儔僼偱丆僇 係丂偳偺僠乕儉傕係帋崌偢偮偩偐傜丆 丂丂丂4亊5亐2亖10帋崌 丂丂丂乮俀偱妱傞偺偼丆廳暋偟偰偄傞偐傜乯 俆丂(傾)丂俙俠2亖俙俢2亄俠俢2傛傝丆 丂丂丂丂丂俙俠亖併(22亄32)亖併13cm 丂丂(僀)丂崅偝傪倛偲偡傞偲懳妏慄偼丆 丂丂丂丂併(22亄32亄倛2)亖7 丂丂丂丂俀忔偟偰丆4亄9亄倛2亖49傛傝丆 丂丂丂丂丂丂丂倛亖6 丂丂丂丂傛偭偰丆1/2亊併13亊6亖3併13cm3 |
44孎杮導 | 侾丂1/4亊1/2亖1/8 俀丂亅12亄8亖亅4 俁丂(亅2倎)亊(亅倎)亖2倎2
俆丂倎2亄2倎倐亄倐2亅倎2亅2倎倐亖倐2
|
|||||||||||||||||||||||||||||
| 42挿嶈導 | 丂丂丂丂亂俙亃 侾丂1亄4亖5
係丂6倎亄2倐亅5倎亖倎亄2倐 俆丂3倶3倷2 俇丂梌幃亖倎2亅2倎2亄倎倐亖亅倎2亄倎倐 丂丂丂丂亖亅(亅3)2亄(亅3)亊2亖亅15 俈丂5倶亖2傛傝丆倶亖2/5 俉丂(倶亅3)(倶亄2)亖0傛傝丆倶亖3丆亅2 俋丂(1)丂倷亖60倶丂斾椺 丂丂(2)丂倷亖10亅4倶丂堦師娭悢 丂丂(3)丂倷亖10/倶丂斀斾椺 丂丂(4)丂倷亖4亅倶丂堦師娭悢 丂丂丂傛偭偰丆乮俁乯 10丂360亅(180亅60)亅(180亅80) 丂丂丂丂亅55亖85亱 丂丂丂丂丂亂俛亃
丂丂偡側傢偪丆値亖5亊2亖10 俆丂2倶2亄5倶亅倶2亄4亖0 丂丂倶2亄5倶亄4亖0 丂丂乮倶亄1)(倶亄4)亖0傛傝丆倶亖亅1丆亅4 俇丂倶亖亅2偺偲偒丆倷亖亅(亅2)2亖亅4 丂丂倶亖1偺偲偒丆倷亖亅12亖亅1 丂丂傛偭偰丆亅4亝倷亝0  俈丂佢倶亖(128亅40)亅55亖33亱 俈丂佢倶亖(128亅40)亅55亖33亱俉丂塃恾 丂嘆俙偐傜屖傪堷偒丆岎揰傪 丂丂俹丆俻偲偡傞 丂嘇俹偲俻偐傜屖傪堷偒丆 丂丂岎揰傪俼偲偡傞 丂嘊 |
45媨嶈導 | 侾丂亅13 俀丂亅20/24亖亅5/6 俁丂6倎亄3倐亅2倎亄8倐亖4倎亄11倐 係丂併54亅併24亖3併6亅2併6亖併6 俆丂忋幃亊3亄壓幃傛傝丆8倶亖40 丂丂丂偙傟偐傜丆倶亖5丆倷亖亅1 俇丂(倶亅3)(倶亅7)亖0傛傝丆倶亖3丆7 俈丂倎亐5亖倐丒丒丒4丂傛傝丆 丂丂丂倎亖5倐亄4丂乮倎亅5倐亖4側偳傕壜乯 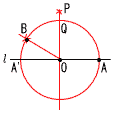 俉丂塃恾 俉丂塃恾丂嘆丂敿宎俷俙偺墌俷傪偐偔 丂嘇丂俙偲俙'偐傜屖傪偐偒丆 丂丂岎揰傪俹偲偡傞 丂嘊丂悅慄俷俹傪傂偒丆 丂丂墌偲偺岎揰傪俻偲偡傞 丂嘋丂俷偲俻偐傜屖傪偐偒丆 丂丂岎揰傪俛偲偡傞 |
|||||||||||||||||||||||||||||
| 46幁帣搰導 | 侾丂(1)丂80亅42亖38
丂丂(4)丂亅2倎倐亊3倐亖亅俇倎倐2
俁丂倎亖亅1丆亅2丆亅3丆亅4丆亅5 丂丂傛偭偰丆倐亖1亅倎亖2丆3丆4丆5 丂丂(倎丆倐)亖(亅1丆2)丂(亅2丆3)丂(亅3丆4) 丂丂丂丂丂丂丂(亅4丆5)丂偺偄偢傟偐 係丂倎亖倶倷亖(亅4)亊(亅2)亖8 丂丂丂倷亖8/倶偵丆倶亖3傪戙擖偟偰丆 丂丂丂倷亖8/3 俆丂佢俛俷俠亖180亅40亊2亖100亱 丂丂仮俙俛俢偱丆佢倶亖30亄100亐2亖80亱 |
|||||||||||||||||||||||||||||||
| 43戝暘導 | 侾丂(1)丂亅7丂丂(2)丂亅3亅10亖亅13 丂丂(3)丂4倶亅10倷亅7倶亄9倷亖亅3倶亅倷 丂丂(4)丂3併2亅5併2亄4併2亖2併2 丂丂(5)丂72倶5倷3亐9倶2倷2亖8倶3倷 俀丂(倶亅7)(倶亄2)
丂丂亖乮屖DF偺墌廃妏乯偩偐傜丆 丂佢EBF=70亅38亖32亱
丂丂偡側傢偪丆値亖2丆8丆18丆72 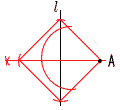 俇丂塃恾 俇丂塃恾丂嘆A偐傜悅慄傪堷偔 丂嘇尨揰O偐傜OA偺挿偝傪偲傞 丂嘊惓曽宍偺捀揰偑寛傑傞 |
47壂撽導丂 | 侾丂3亅5亖亅2
係丂3倎亊4倎2亖12倎3 俆丂15倶亅3亅2倶亄4亖13倶亄1 俇丂2併3亄5併3亖7併3 丂乣丂俀斣栤戣偺堦晹丂乮偍傑偗)丂乣 侾丂3倶亖12傛傝丆倶亖4 俀丂(倎亄2)(倎亄3)亖倎2亄5倎亄6 俁丂3倷亖亅2倶亄4
俆丂(倶亅9)(倶亄2) 俇丂3倶亖21傛傝丆倶亖7 丂丂 |
| 乵僩僢僾偵栠傞乶 乵慜儁乕僕偵栠傞乶 |
丂