全国公立高校入試 　１番問題　【平成２１年春】

（２５）　滋賀県

学習日　 　　 月　　 　　日（　　　　）

PDF版全問題

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１	(1)　2×(−5)＋8 　　　　　　　　　　　　　　　　　　　　　　　　　 . (2)　 ２ ａ− １ ａ ３ ５ 　　　　　　　　　　　　　　　　　　　　　　　　　 . (3)　3(2ｘ＋ｙ)−(4ｘ−5ｙ) 　　　　　　　　　　　　　　　　　　　　　　　　　. (4)　(9ａ2ｂ−6ａｂ2)÷3ａｂ 　　　　　　　　　　　　　　　　　　　　　　　　　 . (5)　(√5−3)(√5＋4)−√45 　　　　　　　　　　　　　　　　　　　　　　　　　 .	３	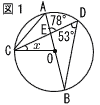図１のように，線分ＡＢを直径とする円Ｏの周上に点Ｃ，Ｄがあり，線分ＡＢとＣＤの交点をＥとする。∠ＢＤＥ＝53°，∠ＡＥＤ＝78°のとき，∠ｘの大きさを求めなさい。 　　　　　　　　　　　　　　　　　　　　　　.
		４	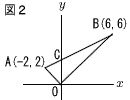図２のように，座標平面上に２点Ａ(−2，2)，B(6，6)をとり，△OABをつくる。 (1)　さいころを２回投げ，１回目に出た目の数をｘ，２回目に出た目の数をｙとして点P(ｘ，ｙ)を取る。このとき，点Pが△OABの周上にある確率を求めなさい。ただし，さいころの１から６のどの目が出ることも同様に確からしいとする。 　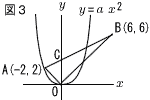　　　　　　　　　　　　　　　　　　　　　　　　. (2)　図３のように，直線ABとｙ軸との交点をCとし，点Aを通るｙ＝ａｘ2のグラフをかく。このグラフ上に△ＯＡＢ＝△ＯＣＱとなる点Ｑをとるとき，点Ｑの座標をすべて求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
２	次の２次方程式を解きなさい。 　　　ｘ2−16＝6ｘ 　　　　　　　　　　　　　　　　　　　　　　　　　 .	５	【　省　略　】