全国公立高校入試
　１番問題　【平成２０年春】
　（４３）　大分県 　学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１ (1)　−6＋2


　　　　　　　　　　　　　　　　　　　　　　　　　 .

(2)　32ｘ3ｙ4÷8ｘｙ2×(ｘｙ)2



　　　　　　　　　　　　　　　　　　　　　　　　　 .

(3)　7√5＋√20−√125


　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　		 ４ 　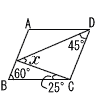右の図のように，平行四辺形ＡＢＣＤにおいて，∠ＡＢＣ＝60°，∠ＢＣＥ＝25°，∠ＣＤＥ＝45°のとき，∠ＣＥＤ＝∠ｘとして，∠ｘの大きさを求めなさい。



　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
５ 　56にできるだけ小さい自然数ｎをかけて，その積がある自然数の２乗になるようにしたい。このときのｎの値を求めなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
２ 　ａ＝√3＋1，ｂ＝√3−1のとき，ａｂの値を求めなさい。




. 　　　　　　　　　　　　　　　　　　　　　　　 .
 ６ 　下の図のように，線分ＡＢと点Ｃがある。この線分ＡＢを弦にもち，点Ｃを通る円を作図しなさい。ただし，作図にはコンパスと定規を用い，作図に使った線は消さないこと。

　　
３ 　２次方程式　x2＋ａｘ＋10＝0　の解の１つが２であるとき，ａの値を求めなさい。また，他の解を求めなさい。





　　　　　　　　　　　　　　　　　　　　　　　　　 .

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい