全国公立高校入試
　１番問題　【平成２０年春】
　（３１）　鳥取県 　学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１ (1)　−4＋9−3

　　　　　　　　　　　　　　　　　　　　　　　　　 .
(2)　 2 ＋ 1 ×2
3 4
　　　　　　　　　　　　　　　　　　　　　　　　　 .

(3)　32＋(−32)＋(−3)2

　　　　　　　　　　　　　　　　　　　　　　　　　 .

(4)　2(3ｘ−4)−(ｘ＋2)

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　		 ６ 　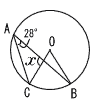右の図の円Ｏで，ＡＣ//ＯＢであるとき，∠ｘの大きさを求めなさい。


　　　　　　　　　　　　　　　　　　　　　　.
　　
７ 　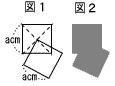１辺がａcmの正方形の紙が２枚ある。右の図１のように，一方の紙の対角線の交点に，もう一方の紙の頂点の１つを重ねて置き，このときできる図形に，図２のように上から色を塗る。
　色を塗った図形の面積が112cm2となるとき，ａの値を求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
２ 　次の連立方程式を解きなさい。
　｛　 3ｘ＋4ｙ＝1
2ｘ−ｙ＝8

. 　　　　　　　　　　　　　　　　　　　　　　　 .
 ８ 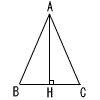右の図の△ＡＢＣは，ＡＢ＝ＡＣの二等辺三角形である。頂点Ａから底辺ＢＣに垂線ＡＨをひくとき，ＢＨ＝ＣＨとなることを証明しなさい。
［証明］
３ 　ｙはｘに比例し，ｘ＝2のときｙ＝−6である。また，ｘの変域が−2≦ｘ≦1のとき，ｙの変域はａ≦ｙ≦ｂである。このとき，ａ，ｂの値を求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
４ 　大小２個のさいころＡ，Ｂを同時に投げ，Ａのさいころの出た目をａ，Ｂのさいころの出た目をｂとする。このとき，ｂ/ａの値が整数となる確率を求めなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　.
　　		 ９ 　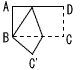右の図は，長方形ＡＢＣＤを頂点Ｄが頂点Ｂと重なるように折り返したときの様子を表した図である。
　この折り返しにより，頂点Ｃが移った点をＣ’とするとき，点Ｃ’の位置を定規とコンパスを使って右下図に作図しなさい。
　なお，作図に用いた線は消さずに残しておきなさい。
５ 　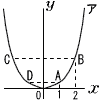右の図において，アは関数　ｙ＝ａｘ2のグラフを表す。点Ａ，Ｂはア上の点であり，そのｘ座標は，それぞれ1，2である。また，点Ｃ，Ｄもア上の点であり，線分ＡＤ，ＢＣは，それぞれｘ軸と平行である。
　４点Ａ，Ｂ，Ｃ，Ｄを頂点とする四角形ＡＢＣＤの面積が6となるとき，ａの値を求めなさい。
　　　　　　　　　　　　　　　　　　　　　　　　　 .

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい