全国公立高校入試 　１番問題　【平成２０年春】

（２７）　大阪府

学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

Ａ　　選　　択		Ｂ　　選　　択
１	3＋(−10) 　　　　　　　　　　　　　　　　　　　　　　　　　 .	１	7−5×3−8÷(−4) 　　　　　　　　　　　　　　　　　　　　　　　　　 .
２	9ａ−2ｂ−(ａ−5ｂ) 　　　　　　　　　　　　　　　　　　　　　　　　　 .	２	3ａ＋ｂ − ａ−ｂ 　　4　 　6　 　　　　　　　　　　　　　　　　　　　　　　　　　.
３	√20−√5 　　　　　　　　　　　　　　　　　　　　　　　　　.	３	ｘ＝1＋3√3，ｙ＝−2＋√3のとき，ｘ２−6ｘｙ＋9ｙ２　の値を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
４	(ｘ＋3ｙ)(ｘ−3ｙ) 　　　　　　　　　　　　　　　　　　　　　　　　　.	４	ａを自然数とするとき，√(4950ａ)の値が自然数となるような最も小さいａの値を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
５	ｘ２＋3ｘ−28　を因数分解しなさい 　　　　　　　　　　　　　　　　　　　　　　　　　.	５	二つの箱Ａ，Ｂがある。箱Ａには偶数の書いてある４枚のカード［２］，［４］，［６］，［８］が入っており，箱Ｂには奇数の書いてある４枚のカード［１］，［３］，［５］，［７］が入っている。箱Ａから１枚のカードを，箱Ｂから２枚のカードを同時に取り出すとき，取り出した３枚のカードに書いてある数のうちで，箱Ａから取り出したカードに書いてある数が最も大きい数である確率はいくらですか。Ａ，Ｂそれぞれの箱において，どのカードが取り出されることも同様に確からしいものとして答えなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
６	奇数の書いてある５枚のカード［１］，［３］，［５］，［７］，［９］が箱に入っている。この箱から２枚のカードを同時に取り出すとき，取り出した２枚のカードに書いてある数の和が一けたの数である確率はいくらですか。どのカードが取り出されることも同様に確からしいものとして答えなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
７	下のア〜エの式表される関数のうち，次の�@の条件をみたすもの，�Aの条件をみたすものはそれぞれどれですか。一つずつ選び，記号を書きなさい。 �@　グラフが(2，−3)を通る。 �A　ｘの値が2から4まで増加するときの変化の割合が3である。 ア　ｙ＝2ｘ−3　　　　イ　ｙ＝−2ｘ＋1 ウ　ｙ＝ １ ｘ２　　　エ　ｙ＝ １ ｘ２ ２ ３ 　　　　　　　　　　　　　　　　　　　　　　　　　.	６	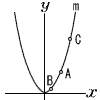右図において，ｍは関数ｙ＝ｘ２のグラフを表す。Ａ，Ｂ，Ｃはｍ上の点である。Ｂのｘ座標はＡのｘ座標より１大きい。直線ＢＣの傾きが３となるときのＡのｘ座業を求めなさい。求め方も書くこと。必要に応じて解答欄の図を用いてもよい。 　　　　　　　　　　　　　　　　　　　　　　　　　.

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい