|
(5) 山形県 | 学習日 月 日( ) |
|
(5) 山形県 | 学習日 月 日( ) |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)〜
| 1 | .
. (3) (12xy−3x)÷3x . (4) (3−√5)(2+√5) . |
4 | 晴美さんは,次の図の∠C=90°の△ABCをもとに,下の【条件】のア,イをともにみたす長方形BCPQをつくりたいと考えた。晴美さんがつくりたいと考えた長方形BCPQの2つの頂点P,Qの位置を,定規とコンパスを使って作図しなさい。 ただし,作図に使った線は残しておくこと。 【条件】 ア 長方形BCPQの面積は,△ABCの面積に等しい。 イ 点Pは,△ABCの辺AC上にある。 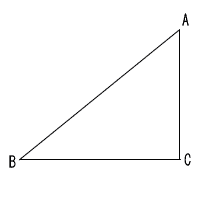 |
||||||||||
| 5 | 下の(A),(B)のどちらか1問を選び,答えなさい。 | ||||||||||||
| 2 | 2次方程式 (x+3)(x−1)=5x+7 を解きなさい。解き方も書くこと。 . . |
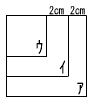 (A) (A). 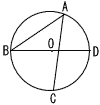 (B) 右の図において,4点A,B,C,Dは点Oを中心とする円の周上にあり,BDはこの円の直径である。円の半径が3cmで,∠BAC=50°であるとき,点Aをふくまない弧CDの長さは何cmか,求めなさい。 (B) 右の図において,4点A,B,C,Dは点Oを中心とする円の周上にあり,BDはこの円の直径である。円の半径が3cmで,∠BAC=50°であるとき,点Aをふくまない弧CDの長さは何cmか,求めなさい。ただし,円周率はπとする。 . |
|||||||||||
| 3 | 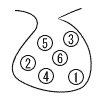 右の図のように,袋の中に,1から6までの数字を1つずつ書いた玉が6個入っている。この袋から,玉を1個取り出して,その玉に書かれている数字を調べ,それを袋にもどしてから,また,玉を1個取り出して,その玉に書かれている数字を調べる。 右の図のように,袋の中に,1から6までの数字を1つずつ書いた玉が6個入っている。この袋から,玉を1個取り出して,その玉に書かれている数字を調べ,それを袋にもどしてから,また,玉を1個取り出して,その玉に書かれている数字を調べる。はじめに取り出した玉に書かれている数字を十の位の数,次に取り出した玉に書かれている数字を一の位の数として,2けたの整数をつくるとき,45以上の整数になる確率を求めなさい。 ただし,どの玉が取り出されることも同様に確からしいものとする。 . |
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |