|
正 答 ６ | |||
| 41 佐賀県 〜 47 沖縄県 |
|
正 答 ６ | |||
| 41 佐賀県 〜 47 沖縄県 |
| 41佐賀県 | １ (ア) ７＋１１＝１８ (イ) ２ａ−４ｂ−６ａ＋９ｂ＝−４ａ＋５ｂ (ウ) √１８＋√９−√８ ＝３√２＋３−２√２＝３＋√２ ２ ｘ＝−３を代入して， (−３)２−(−３)ａ−１５＝０ ９＋３ａ−１５＝０より，ａ＝２ ３ Ａ・・・ｘ＝４を代入して，ｙ＝−８ Ｂ・・・ｘ＝−１を代入して，ｙ＝−１/２ Ｃ・・・ｘ＝２を代入して，ｙ＝−２ Ｄ・・・ｘ＝−１/２を代入して，ｙ＝−１/８ したがって，ＡとＤ ４ 赤玉をＲ１〜３，白玉をＷ１〜２とすると， 同色は，Ｒ１Ｒ２，Ｒ１Ｒ３，Ｒ２Ｒ３，Ｗ１Ｗ２ の４通り 異色は，Ｒ１Ｗ１，Ｒ１Ｗ２，Ｒ２Ｗ１，Ｒ２Ｗ２， Ｒ３Ｗ１，Ｒ３Ｗ２の６通り 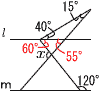 したがって，４÷（４＋６）＝２/５ ５ 平行より，赤左が６０° 外角より，赤右が５５° ∠ｘ＝６０＋５５＝１１５° |
45宮崎県 | １ ２−５＝−３
３ １０ａ−５ｂ−８ａ−２ｂ＝２ａ−７ｂ ４ √１８÷√２＝√９＝３ ５ 両辺×２より， ６ｘ−ｘ＋１＝２１ ５ｘ＝２０で，ｘ＝４ ６ （ｘ＋５）（ｘ−４） ７ ∠ｘ＝２５＋８０＋３０＝１３５° 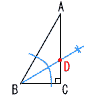 ８ ∠ＣＤＡ＝３０°と なればよい。 ∠Ｂ＝６０°だから， ∠Ｂの二等分線を作図 して，交点をＤとする。 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 42長崎県 | 〜 Ａ問題 〜 １ −１２＋２＝−１０
４ ５ａ＋ｂ ５ ４ｙ ６ ２２＋２＝６ ７ 上式＋下式より，ｘ＝２ これを下式に代入して，ｙ＝−１ ｘ＝２，ｙ＝−１ ８ （ｘ−１）（ｘ−３）＝０より，ｘ＝１，ｘ＝３ ９ ｙ＝ａｘに（３，６）を代入して，６＝３ａ ａ＝２より，ｙ＝２ｘ 10 ６：９＝ｘ：１２より，ｘ＝８ 〜 Ｂ問題 〜 １ ２√６−２＋３−２√６＋２＝３
これを代入して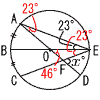，ｙ＝−１  ｘ＝３，ｙ＝−１５ ４ｘ２−１−４ｘ−７＝０ ４ｘ２−４ｘ−８＝０ ｘ２−ｘ−２＝０ （ｘ−２）（ｘ＋１）＝０より， ｘ＝２，−１ ６ ＯＡ＝ＯＥより，∠Ａ＝２３° よって，∠ＥＯＦ＝４６° また，弧ＡＢ＝弧ＢＣより，∠ＯＥＦ＝２３° よって，∠ｘ＝４６＋２３＝６９（°） |
46鹿児島県 | １ (1) ３２−３＝２９
(３) ３ａ＋２７−４２＋３０ａ＝３３ａ−１５
３ １５と２４の最小公倍数を求めると，
よって，午前９時３０分 ４ ｙ＝ａ/ｘに（２，−２）を代入して，ａ＝−４ グラフは比例例数が負の双曲線 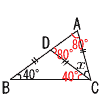 よって，ウ５ ＤＢ＝ＤＣより， ∠ＤＣＢ＝４０° ∠ＣＤＡ＝４０＋４０＝８０° ＣＡ＝ＣＤより，∠Ａ＝８０° ∠ｘ＝１８０−８０×２＝２０° |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 43大分県 | １ (１) −１６ (２) ６ｘ２ｙ
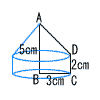 ｘ２−ｘ−６＝０（ｘ−３）（ｘ＋２）＝０より， ｘ＝３，−２ ４ ｘｙ＝ａに（３，４）を代入して ａ＝１２ ｙ＝１２/ｘ ５ 回転体＝円すい＋円柱 ＝１/３×３２π×３ 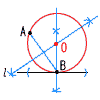 ＋３２π×２＝９π＋１８π ＝２７πｃｍ３ ６ 点Ｂから  の垂線を引く線分ＡＢの垂直二等分線 を引く 交点をＯとして，円Ｏをかく |
47沖縄県 | １ −５
４ ４ａ２×３ａ＝１２ａ３ ５ ８ｘ−５ｙ−６ｘ−２ｙ＝２ｘ−７ｙ ６ ４√３＋２√３＝６√３ 〜 ２番問題の一部（おまけ） 〜 １ １２０×０．８＝９６（円） ２ ２×（−３）＋（−３）２＝−６＋９＝３ ３ ５ｙ＝−３ｘ＋２
５ （ｘ＋１）（ｘ＋５） ６ √１（１）＜√３＜√４（２） よって，√３＝１．××× √２５（５）＜√３０＜√３６（６） よって，√３０＝５．××× したがって，１＜√３０＜６で， この間の整数は，２，３，４，５の４（個） ７ ６ｘ−２ｘ＝−５−１１ ４ｘ＝−１６より，ｘ＝−４ |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 44熊本県 | １ ３．２ ２ −１/６ ３ ５ａ−７＋２ａ−１＝７ａ−８ ４ ３ｘ×４ｘ＝１２ｘ２ ５ ａ２＋ｂ２−ａ２＝ｂ２ ６ √１０００−√１０＝１０√１０−√１０ ＝９√１０ |
