|
正 答 1 | |||
| 1 北海道 〜 8 茨城県 |
|
正 答 1 | |||
| 1 北海道 〜 8 茨城県 |
| 1北海道 | 1 (1) −1 (2) −4+7=3 (3) 6+(1/9)×9=6+1=7 2 3x−12xy 3 (7−4a)−(2a+1)=7−1−4a−2a=6−6a 4 与式に(1,−2)を代入すると, 
ウをアに代入して,6+2b=14で,b=4 よって,a=6,b=4 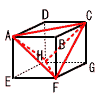 5 y=−5x+8+9より,y=−5x+17 5 y=−5x+8+9より,y=−5x+176 (右上図参照) 重なる線分の中点Mをとり, Mを通る直線を引く。 7 (右図参照) ア〜ウはC,F,H エ 5√2cm (1辺5cmの正方形の対角線の長さを求める) |
4岩手県 |  1 7−6=1 1 7−6=12 a+1−2a+3=−a+4 3 3√2+√2=4√2 4 (x−3)(x+2)=0より,x=3,−2 〜2番問題(おまけ)〜 1 5と7 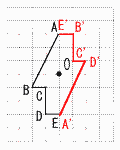 2 (右上図参照) 2 (右上図参照)A+0+1=6より,A=5 3 x=−4のとき,y=−(−4)+3=7 x=3のとき,y=−3+3=0 よって,0≦y≦7 4 (右図) 黒線図形ABCDEの各頂点から 中心Oに関して点対称となる A’〜E’をとる |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2青森県 |
2 6x−2x+5=11より,4x=6で,x=6/4=3/2 3 両辺×4より,4m=a+3b
5 2点A,Bは双曲線上の点だから,原点対称 A(2−4)となるから, a(比例定数)=xyより,a=2×(−4)=−8
x+28+47+(360−131)=360 x=131−28−47=56° 7 円すいの高さは,√132−52=12cm 円柱の高さをhとすると, 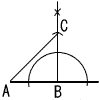 52πh×(1/5)=(1/3)×52π×12 52πh×(1/5)=(1/3)×52π×125πh=100πで,h=20cm 8 (右図参照) (1) Bから垂線をかく (2) BA=BCとなる点Cをとる (3) AとCを結ぶ |
5山形県 | 1 (1) 4+8−5=7
(4) 3−2√6+2−2√6=5−4√6
2 x2−x−6=x+9で, 移項してx2−2x−15=0 (x−5)(x+3)=0より,x=5,−3 3 積を右の表にまとめると, −2以上(赤字)は19個だから, 19/25 4 (右下図) (1) モミの木から垂線を引く (2) モミと松の木の距離の2倍の長さを 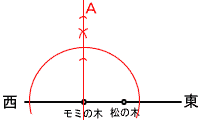 垂線上に点Aをとる 垂線上に点Aをとる5(A) x=1のとき, y=12a=a x=3のとき, y=32a=9a
5(B) △EAF∽△ECDより,AF:4=5:3 3AF=20で,AF= 20/3 cm |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3秋田県 | 1 (1) 4−6=−2 (2) (−8)÷2=−4 2 (1) 80−a (cm) (2) b−3a (cm)
6 移項して整理すると,x2−5x−14=0 (x−7)(x+2)=0より,x=7,−2 7 3√2+3−2√2=√2+3 8 根号内=4(31−2a)となるから, 31−2aが平方数になればよい。 31−2a=25,16,9,4,1,0の場合を調べると, 31−2a=25のとき,a=3 31−2a=9のとき, a=11 31−2a=1のとき,a=15 よって,a=3,11,15 9 中央の自然数をxとすると, (x−1)2+x2+(x+1)2=365 これを解くと,x=11 よって,10,11,12 10 男子x人,女子y人とすると, 166.3x+158.3y=162.7(x+y) これを解くと,5.6x=4.4y x;y=4.4:5.6=44:56=11:14 11 ∠x=180−(40+75)=65° 12 ∠OAC=∠ACO=34°より, ∠x=34×2=68° 13 AF=EF=xcmとすると,BF=10−x △FBEで,(10−x)2+52=x2
14 半径AD=r,高さAB=hとすると,
 15 (右図参照) (1) 線分ABの垂直二等分線mを引く (2) 適当な弦CDの垂直 二等分線nを引く (3) mとnの交点O(左の円の中心) をとる (4) m上にMO=MO’の点O’をとる (5) O’を中心とする弧をかく |
6宮城県 | 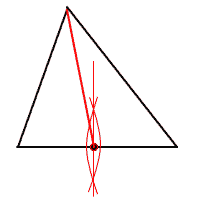 1 −9+2=−7 1 −9+2=−7
3 m=3n+2 4 2√7=√28で,√25<√28<√36 5<√28<6となるから,1,2,3,4,5 5 (右図) 辺の中点をとり,中線を引けばよい |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7福島県 |
〜2番問題(おまけ)〜 1 上式×2+下式より,5x=20で,x=4 これを下式に代入して,4+2y=6で,y=1 よって,x=4,y=1 2 △ACDは底角57°の二等辺三角形だから, ∠x=180−57×2=66° 3 y=axに,(2,14)を代入すると, 14=2aで,a=7 よって,y=7x 4 5人から2人選ぶ方法は,5×4÷2=10通り このうち,Aがふくまれるのは4通り
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8茨城県 | 1 (1) −7 (2) −2−10=−12
(5) 6+8√3−√3−4=2+7√3 〜2番問題(おまけ)〜 1 (x−9)(x+2) 2 x=7,y=10 3 (x+2)(x+3)=0より,x=−2,−3 4 y=ax+bに,(−6,1)と(3,7)を代入すると,
|