|
(31) 鳥取県 | 学習日 月 日( ) |
|
(31) 鳥取県 | 学習日 月 日( ) |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4が2枚になります)〜
| 1 | (1) .
(3) 3(x+1)−2(x−4) . (4) (−a)2×8a . |
6 | 「xの値が1から3まで増加したときの変化の割合が−2である」という条件にあてはまる関数の式を,次のア〜エの中からすべて選び,記号で答えなさい。 ア y=−2x イ y=x−2 ウ y=−2x2
. |
|||||||||
| 7 | 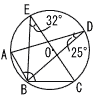 . |
|||||||||||
| 2 |
. |
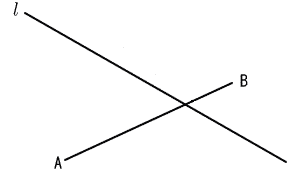
8 | 下の図のように,線分ABと直線 なお,作図に用いた線は消さずに残しておきなさい。 |
|||||||||
| 3 | 二次方程式 (x−2)2=−2x+7 を解きなさい。 . |
 |
||||||||||
| 4 | A,B2つのさいころを同時に投げ,Aのさいころの出た目の数をa,Bのさいころの出た目の数をbとする。 (1) ab=12となるのは,何通りあるか求めなさい・ . (2) . |
|||||||||||
| 5 | 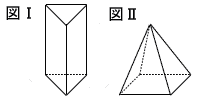 . |
9 | 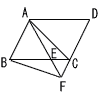 右の図の平行四辺形ABCDにおいて,辺BC上に点Eをとり,直線AEと辺DCの延長との交点をFとする。 右の図の平行四辺形ABCDにおいて,辺BC上に点Eをとり,直線AEと辺DCの延長との交点をFとする。このとき,△AECと△BEFの面積が等しいことを証明しなさい。 |