|
（５） 山形県 | 学習日 月 日（ ） |
|
（５） 山形県 | 学習日 月 日（ ） |
〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜
| １ | (１)  ４−（−８)−５.
. (３) （６ａ２−１５ａｂ）÷３ａ . (４) （√3−√2）２−√24 . |
４ | ある中学校で，卒業記念として校庭に桜の木を１本植えることにし，植える位置については，下の【条件】のア，イをともに満たすこととした。図は，校庭を上から見たものである。桜の木を植える位置をＡとし，定規とコンパスを使って，図に位置Ａを作図しなさい。ただし，作図に使った線は残しておくこと。なお，モミの木と松の木の位置は点で示してあり，図のモミの木と松の木を通る直線は東西にのびている。 【条件】 ア 桜の木は，モミの木の真北に植える。 イ 桜の木とモミの木との距離は，モミの木と松の木との距離の２倍とする。  |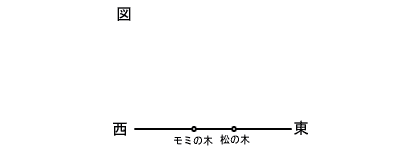
|||||||||
| ２ | ２次方程式 （x＋２）（x−３）＝x＋９ を解きなさい。解き方も書くこと。 . |
５ | ＜選択問題＞ 次の(Ａ)，(Ｂ)のどちらか１問を選び，答えなさい。 (Ａ) 関数 y＝ax２ について，xの値が１から３まで増加するときの変化の割合が２であった。このとき，aの値を求めなさい。 . 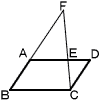 (Ｂ) 右の図で,平行四辺形ＡＢＣＤの辺ＡＤ上に点Ｅがあり,線分ＣＥをＥの方へ延長した線と，線分ＢＡをＡの方へ延長した線との交点がＦである。ＡＢ＝４ｃｍ，ＡＥ＝５ｃｍ，ＤＥ＝３ｃｍであるとき，ＡＦの長さを求めなさい。 . |
|||||||||
| ３ | 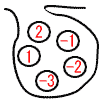  右の図のように，袋の中に、整数の，２，１，−１，−２，−３を１つずつ書いた玉が５個入っている。いま，この袋から，同時に２個の玉を取り出し，それぞれの玉に書かれている整数の積を求めるとき，その積が−２以上になる確率を求めなさい。ただし，どの玉が取り出されることも同様に確からしいものとする。 . |
