|
正 答 ６ | |||
| 41 佐賀県 〜 47 沖縄県 |
|
正 答 ６ | |||
| 41 佐賀県 〜 47 沖縄県 |
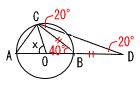
| 41佐賀県 | １ （ア） −３＋７＝４ （イ） ３ｘ−６ｙ＋５ｘ−３ｙ＝８ｘ−９ｙ （ウ） ５−３＝２ ２ ｘ２−３ｘ＝０より，ｘ（ｘ−３）＝０ ｘ＝０，３ ３ ｘｙ＝ａに（４，６）を代入すると， ａ＝４×６＝２４で，ｙ＝２４/ｘ これにｘ＝８を代入して，ｙ＝３ ４ （大，小）＝（２，６）（６，２）（３，４）（４，３） （４，６）（６，４）（６，６）の７通りあるから， ７/３６ ５ 円Ｏの中心とＢ，Ｃを結ぶと， △ＯＡＢは正三角形となるから，∠ＢＯＣ＝６０° よって，∠ＢＡＣ＝６０÷２＝３０° |
45宮崎県 | 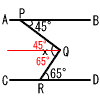 １ −７＋９＝２ ２ −２/３３ ａ＋５−６＋３ａ＝４ａ−１ ４ ５√３−４√３＋√３＝２√３ ５ （ｘ−１）（ｘ−５）＝０ ｘ＝１，５ ６ (2，−3)を通る反比例の グラフだから， 比例定数ａ＝ｘｙ＝２×（−３）＝−６
 ７ 右図より，∠ｘ＝４５＋６５＝１１０° ８ １ ＡＢの垂直二等分線 ２ ＯＡを半径とする円 ３ 垂直二等分線と円の 交点をＣ，Ｄとする ４ 四角形ＡＤＢＣが 求める正方形 |
|||||||||||||||||||||||||||||||||||||||||||
| 42長崎県 | １ １−３＝−２
５ 式を簡単にしてから代入する 与式＝１０ａ−４ｂ−９ａ＋３ｂ＝ａ−ｂ ＝−２−３＝−５ ６ （２ｘ＋５）（２ｘ−５） ７ 上式×２＋下式より，７ｘ＝１４ ｘ＝２ これを下式に代入すると， ６＋２ｙ＝４より，ｙ＝−１ したがって，ｘ＝２，ｙ＝−１ ８ ＡＢ間の距離は，６０×２０＝１２００ｍ
|
46鹿児島県 | １ （１） １０−１．７＝８．３
Ａ＝１，Ｂ＝−１ とか Ａ＝−１，Ｂ＝−３ ４ １．２ｘ＝１０２より，
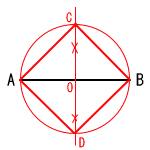
 ５ △ＢＣＤは二等辺三角形になるから， ∠ＡＢＣ＝４０° よって，∠ｘ＝４０×２＝８０° |
|||||||||||||||||||||||||||||||||||||||||||
| 43大分県 | 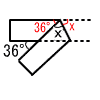 １ （１） −３ （２） −４ｘ２ｙ（３） ３√２＋４√２＝７√２ ２ ｘ２＋ｘ−６−５ｘ＋１＝０ ｘ２−４ｘ−５＝０ （ｘ−５）（ｘ＋２）＝０ ｘ＝５，−１ ３ ア と エ 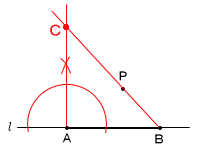 ４ 右図参照して，∠ｘ＝（１８０−３６）÷２＝７２° ５ ア 青，イ 黄，ウ 赤 ６ まずＡを通る垂線を作図する 次にＢからＰを通る直線を引く ２本の直線の交点をＣとする |
47沖縄県 | １ ５
３ ２−５＝−３ ４ ａ×９ａ２＝９ａ３ ５ ４ｘ２＋８ｘ−４＋３ｘ２−３ｘ−６ ＝７ｘ２＋５ｘ−１０ ６ ６√５−２√５＝４√５ ［２番問題 おまけ］ １ ２）２４ ５４ ３）１２ ２７ ４ ９ したがって，２×３＝６ ２ １５００×１．２＝１８００円 ３ ７ｙ＝２ｘ−５
５ 上式を下式に代入して，３ｘ−２（ｘ−３）＝８ ｘ＝２ これを下式に代入して，ｙ＝２−３＝−１ ｘ＝２，ｙ＝−１ ６ ｘ＝−２を元に式に代入して， ６＋ａ＝−４＋１７より，ａ＝７ ７ （２ａ＋７）（２ａ−７） ８ （ｘ−５）２＝３より，ｘ−５＝±√３ ｘ＝５±√３ |
|||||||||||||||||||||||||||||||||||||||||||
| 44熊本県 | １ ６ ２ ８ ３ −８×５＝−４０ ４ １２ａ＋３ｂ−７ａ＋ｂ＝５ａ＋４ｂ ５ ｘｙ−２
［２番問題の一部］ １ 上式を下式に代入すると， ４ｘ＋３（６ｘ＋９）＝５ ４ｘ＋１８ｘ＝５−２７ ２２ｘ＝−２２より，ｘ＝−１ これを上式に代入して， ｙ＝−６＋９＝３ ｘ＝−１，ｙ＝３ ２ ｘ（４ａ２−９）＝ｘ（２ａ＋３）（２ａ−３） |
