|
正 答 １ | |||
| １ 北海道 〜 ８ 茨城県 |
|
正 答 １ | |||
| １ 北海道 〜 ８ 茨城県 |
| １北海道 | １ （１） ８−４＝４
＝（√６）２＝６ ４ ｘｙ＝ａに，ｘ＝５ ｙ＝４を代入して，ａ＝２０ ｘｙ＝２０に，ｘ＝２を代入して，ｙ＝１０
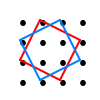 ６ ∠ＡＰＢ（円周角）＝１２４÷２＝６２°７ １２＋２２＝（√５）２となるから， 直角をはさむ２辺が１ｃｍと２ｃｍの 三角形を考えてつくればよい。 右図の赤と青の２個 |
５山形県 | １ （１） ６＋５＝１１
２ ｘ２−４＝−４ｘ＋１より，（ｘ＋５）（ｘ−１）＝０ よって，ｘ＝−５，１ ３ 直径ＰＱと交わる線分は， ＡＤ，ＡＥ，ＢＤ，ＢＥ，ＣＤ，ＣＥの６本だから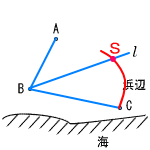，  ６÷１０＝３/５４ ∠ＡＢＣの２等分線  を引き，上にＢＳ＝ＢＣとなる点Ｓをとる。 ５ Ａ（−6，0） Ｂ（0，12）より， Ｃ（6，12）となるから， ｙ＝ａｘ２に点Ｃの座標を 代入すると， 12＝ａ×62より，ａ＝1/3 |
|||||||||||||||||||||||||||||||||||||
| ２青森県 | 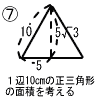 １ ア −4 イ 10 ウ 0エ 24ｘ２ｙ÷3ｘ＝8ｘｙ オ 49−ａ２ ２ 5ｘ−15＝3ｘ−10 2ｘ＝5より， ｘ＝5/2（または2.5） ３ 4（3ａ−2ｂ）−（5ａ−4ｂ）＝7ａ−4ｂ ４ 4√3＋□−3√3＝2√3 □＝2√3−4√3＋3√3＝√3 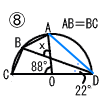 ５ （ｘ−４）２＝０ となればいいから，ｘ２−８ｘ＋１６＝０ より， ａ＝−８，ｂ＝１６ ６ ｘ＝−４のとき，ｙ＝８となるから， ０≦ｙ≦８ ７ 12×10×5√3×8＝200√3ｃｍ２ ８ ∠ADC=４４°より，８８−２２＝６６° |
６宮城県 | １ −５＋２＋４＝１ ２ ４ｘ−２ｙ−３ｘ＋６ｙ＝ｘ＋４ｙ ３ −５，−４， ４， ５ ４ ｘ2＝ｘ＋２ ｘ2−ｘ−２＝０ 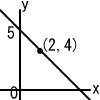 （ｘ−２）（ｘ＋１）＝０ｘ＝２，−１ ５ 右図のように，点（2，4）を通り， 右下がりの直線を考えるとよい。 答は何通りでも考えられるが， そのうち１つを書けばよい。 たとえば，ｙ座標が5で，ｙ＝−ｘ＋5 あるいは，ｙ座標が4で，ｙ＝−1/2ｘ＋4 |
|||||||||||||||||||||||||||||||||||||
| ３秋田県 | １ ５−８＝−３ ２ （１０ａ−２）個
６ ｘ2＋2ｘ−48−15＝0より，(ｘ＋9)(ｘ−7)＝0 ｘ＝−９，７ ７ 与式＝ｘｙ（ｘ−１）＝６√７ ８ √３０＜ｘ＜√８０より，３０＜ｘ２＜８０ となるから， ｘ＝６，７，８
10 （100ａ＋10ｂ＋ｃ）＋（100ｂ＋10ｃ＋ａ） ＋（100ｃ＋10ａ＋ｂ） ＝１１１（ａ＋ｂ＋ｃ）＝１２２１より， ａ＋ｂ＋ｃ＝１１ 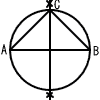 12 （７６−３３）＋２４＝６７°13 三平方の定理より，ＡＤ＝５ △ＡＤＯ∽△ＡＢＣより， ＡＤ：ＡＢ＝ＤＯ：ＢＣで， ＢＣ＝２４/５ 14 （122π−62π）×120/360 ＋42π＋22π＝５６π 15 （右図） |
７福島県 | ［１番問題］ １ （１） −５ （２） −２/３ （３） ４√２−２√２＝２√２ （４） ２ｘ＋６−６ｘ＋３＝−４ｘ＋９ ２ ｙ軸上の切片が−１で，傾きが２の直線だから，ウ ［２番問題 おまけ］ １ （ｘ−７）（ｘ＋１）＝０より，ｘ＝７，−１ ２ ∠ＢＡＤ＝９０°より，∠ＡＤＢ＝９０−３６＝５４° ∠ＡＣＢ＝∠ＡＤＢ＝５４°（円周角）より， ∠ｘ＝９５−５４＝４１° ３ −１，０，１
|
|||||||||||||||||||||||||||||||||||||
| ４岩手県 | ［１番問題］ １ −８＋５＝−３ ２ ２ａ＋６−ａ＋２＝ａ＋８ ３ １６−５＝１１ ４ （ｘ＋５）（ｘ−３）＝０ ｘ＝−５，３ ［２番問題 おまけ］ １ −３，＋３（３も可）
|
８茨城県 | ［１番問題］ １ ５−１０＝−５ ２ −２＋１２＝１０
５ ２√３−２√３＋√６＝√６ ［２番問題 おまけ］ １ （ｘ＋７）（ｘ−２） ２ 下式を上式に代入して，５ｘ＋２（３ｘ＋５）＝−１ よって，ｘ＝−１ これを下式に代入すると， ｙ＝３×（−１）＋５＝２ ｘ＝−１，ｙ＝２ ３ ｘ２−１１ｘ＋３０＝０ （ｘ−５）（ｘ−６）＝０ ｘ＝５，６ ４ 与式＝ｘ（ｘ−４）＝（√３＋２）（√３−２）＝−１ ５ ｘ＝−２のとき，ｙ＝−２×（−２）＋５＝９ ｘ＝４のとき，ｙ＝−２×４＋５＝−３ したがって，−３≦ｙ≦９ |
