17年滋賀県

～印刷して、紙の上でやってネ！（文字サイズを小にするとＡ４に収まります）～

１

（１）　

　４×（－２）＋５

　　　　　　　　　　　　　　　　　　　　　　　　　.
（２）　

　７ａ－（４－５ａ）

　　　　　　　　　　　　　　　　　　　　　　　　　.

（３）　１２ａ^２ｂ^２÷（－２ａ）^２

　　　　　　　　　　　　　　　　　　　　　　　　　.

（４）	２１	＋√２８
	√７

５

　右図のように，関数　ｙ＝２ｘ^２のグラフ上の点Ｐからｘ軸，ｙ軸に垂直な直線をひき，それぞれの軸と交わる点をＡ，Ｂとする。原点をＯとして，四角形ＯＡＰＢが正方形になるときの点Ｐの座標を求めなさい。ただし，点Ｐのｘ座標は正とする。

　　　　　　　　　　　　　　　　　　　　　　　　.
　

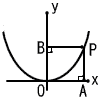６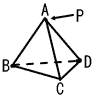

　右図のように，一辺１ｃｍの正四面体の頂点Ａに点Ｐがある。点Ｐは頂点Ａから動き始め，正四面体の辺上を頂点から頂点へ移動する。３ｃｍ動いたとき，点Ｐが頂点Ｂにある経路は何通りあるか，求めなさい。ただし，点Ｐは同じ辺上を繰り返し通ることができるものとする。

　　　　　　　　　　　　　　　　　　　　　　　　.
　

２

　ｘ＝２．４，ｙ＝０．２のとき，次の式の値を求めなさい。
　　ｘ^２－４ｙ^２

　　　　　　　　　　　　　　　　　　　　　　.
　

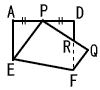
　７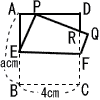

　右図は，ＡＢ＝ａｃｍ，ＢＣ＝４ｃｍ，の長方形ＡＢＣＤをＥＦ折り目として，頂点Ｂが辺ＡＤ上の点Ｐにくるように折り返したものである。このとき，頂点Ｃが移動した点をＱ，ＤＦとＰＱの交点をＲとする。
（１）　△ＰＤＲ∽△ＦＱＲを証明しなさい。

３

　一次関数　ｙ＝ａｘ＋ｂのグラフが２点（１，－１），（２，１）を通るとき，ａ，ｂの値を求めなさい。

　　　　　　　　　　　　　　　　　　　　　.
　

４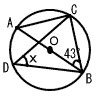

　右図のような，線分ＡＢを直径とする円Ｏがあり，円Ｏの円周上に点Ｃ，Ｄがある。∠ＡＢＣ＝４３°のとき，∠ｘの大きさを求めなさい。

　　　　　　　　　　　　　　　　　　　　.

（２）　

　右図のように，点ＰがＡＤの中点にあるとき，△ＰＤＲと△ＦＱＲの面積が等しくなった。このとき，ａの値を求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　.
　