|
(5) 山形県 3月10日実施/50分 | |||
| 学習日 月 日( ) |
|
(5) 山形県 3月10日実施/50分 | |||
| 学習日 月 日( ) |
~ 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)~
| 1 | (1) .
(3) 3a×(-4ab2)÷6ab (4) (√3-2)(√3+1) |
3 | 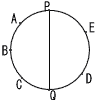 いま,この袋から,同時に2枚のカ-ドを取りだし,そのカ-ドの記号を示す円周上の2点を結ぶ線分をひくとき,その線分が直径PQと交わる確率を求めなさい。ただし,どのカードが取り出されることも同様に確 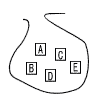 からしいものとする。 からしいものとする。. |
|||||||||
| 4 | 太郎さん,明男さん,一郎さんの3人は,浜辺にある地点Sを出発して,それぞれ地点A,B,Cに着いた。4つの地点S,A,B,Cの間には, ∠SBC=1/2∠ABC,BS=BCの関係があった。定規とコンパスを使って,右の図にSの位置を作図しなさい。 ただし,作図に使った線は残しておくこと。 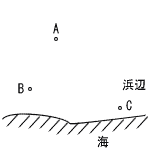 |
|||||||||||
| 2 | 2次方程式(x+2)(x-2)=-4x+1を解きなさい。解き方も書くこと。 . |
5 | 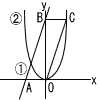 右の図で,①は1次関数 y=2x+12 のグラフ,②は関数 y=ax2 のグラフである。 右の図で,①は1次関数 y=2x+12 のグラフ,②は関数 y=ax2 のグラフである。①とx軸,y軸との交点を,それぞれA,Bとする。②上に点Cをとり,平行四辺形BAOCをつくることができるとき,aの値を求めなさい。 . |