|
（１３） 東京都 ２月２４日実施／５０分 | |||
| 学習日 月 日（ ） |
|
（１３） 東京都 ２月２４日実施／５０分 | |||
| 学習日 月 日（ ） |
〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜
| １ |
. |
７ |  １から６までの目の出る大小１つずつのさいころを同時に投げる。大きいさいころの出た目の数をａ、小さいさいころの出た目の数をｂとするとき、２ａ＋３ｂ＝２０が成り立つ目の出方は全部で何通りあるか。 . |
||||
| ２ | −ａ＋４ｂ−５（ａ−ｂ） . |
||||||
| ３ | （３−√７）（３＋√７） . |
８ | 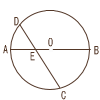 右の図は，線分ＡＢを直径とする円Ｏであり，２点Ｃ，Ｄは，円Ｏの周上にある点である。４点Ａ，Ｂ，Ｃ，Ｄは，右の図のようにＡ，Ｃ，Ｂ，Ｄの順に並んでおり，互いに一致しない。弧ＣＢの長さは円Ｏの円周の長さの１/６倍であり，弧ＤＡの長さは円Ｏの円周の長さの１/１２倍である。 ２点Ｃ，Ｄを結んだ線分と直径ＡＢとの交点をＥとする。鋭角である∠ＢＥＣの大きさは何度か。 . |
||||
| ４ | 一次方程式 ６ｘ＋９＝８ｘ−５ を解け。 . |
||||||
| ５ |
. |
９ | 直線 上にない点Ｐを通り，と垂直に交わる直線を，定規とコンパスを用いて作図せよ。ただし，作図に用いた線は消さないでおくこと。・ Ｐ . |
||||
| ６ | 二次方程式 （ｘ＋１）２＝４ を解け。 . |
