|
(5) 山形県 3月10日実施/50分 | |||
| 学習日 月 日( ) |
|
(5) 山形県 3月10日実施/50分 | |||
| 学習日 月 日( ) |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)〜
| [1] | |||||||||||||
| 1 | .
. (3) 8a2b÷(−6ab)×3b . (4) √12+√3(√6−3) . |
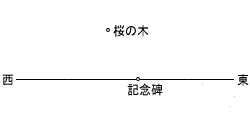
4 | 晴美さんたちが校庭に埋めたタイムカプセルの位置を示す目印がなくなってしまいました。埋めた位置をAとし,下の2人の記憶をもとに,コンパスと定規を使って,あとの図に位置Aを作図しなさい。 ただし,作図に使った線は残しておくこと。なお,記念碑(ひ)と桜の木の位置は点で示してあり,図の記念碑を通る直線は東西にのびている。
|
||||||||||
 |
|||||||||||||
| 2 | 二次方程式 (x+2)(x−1)=2x+4 を解きなさい。解き方も書くこと。 . |
5 | 次の(A),(B)のどちらか1問を選び,答えなさい。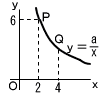 . 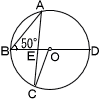 (B) 右の図において,BDは点Oを中心とする円の直径で,∠ABD=50°であり,点Aをふくまない2つの弧BCと弧CDの長さの比は1:2である。線分ACが直径BDと交わる点をEとするとき,∠AEBの大きさを求めなさい。 (B) 右の図において,BDは点Oを中心とする円の直径で,∠ABD=50°であり,点Aをふくまない2つの弧BCと弧CDの長さの比は1:2である。線分ACが直径BDと交わる点をEとするとき,∠AEBの大きさを求めなさい。. |
||||||||||
| 3 | 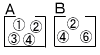 ただし,それぞれの箱において,どの玉が取り出されることも同様に確からしいものとする。 . |
||||||||||||