|
正 答 1 | 1 北海道 〜 8 茨城県 |
|
正 答 1 | 1 北海道 〜 8 茨城県 |
| 1北海道 | 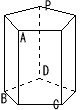 1 (1) −20 (2) 13 (3) 32 1 (1) −20 (2) 13 (3) 322 a2+7ab 3 x=3を代入すると,9+3a−15=0より,a=2 4 y=3x+bに,x=−1とy=2を代入する 2=−3+bより,b=5 y=3x+5 5 ∠D=x とすると, ∠C=2x,∠B=2x,∠A=4xとなる ∠A+∠B+∠C+∠D=4x+2x+2x+x =9x=360°より x=40° ∠A=4x=4×40=160° 6 1と2 1と4 2と3 2と5 3と4 4と5 の 6通り 7 右上の図参照 頂点C |
5山形県 | 1 (1) −2+6=4 (2) (−3/7)×7/15=−1/5 (3) 8x−5y (4) 3√2−2+2√2=5√2−2 2 x2−4x−5+2x+2=0 x2−2x−3=0 (x−3)(x+1)=0より, x=3,−1 3 (P,Q)=(4,1),(3,2),(2,3),(1,4)の4通りだから, 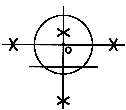 4/36=1/9 4/36=1/94 右図 5 (A) P(2,1),Q(4,4)となるから, △PQR=4×3÷2=6 (B) 三平方の定理より,AH=3 対角線の交点をOとすると,OH=1 OA2=12+32 より,AC=2√10cm |
| 2青森県 | 1 (1) 2+6=5 (2) −2/3(−3分の2) (3) 16−45=−29 (4) 4x5y2 (5) 4√3+2√3=6√3 2 与式=−3a−10b−5b+4a=a−15b =4−15×(−2)=34 3 両辺×3より,3x−(2x+1)=15 x=16 4 2(a2+3a−10)=2(a+5)(a−2) 5 a=xy=4×(−2)=−8より, y=−8/x ア −1/2 6 x=90−32=58° 7 S=3a×2+2a×2+6×2=10a+12 8 AH2=132−122=25より,AH=5 体積は50×12÷3=200cm3 |
6宮城県 | 1 −24÷2=−12 2 −1<−1/3<0 (0>−1/3>−1でもよい) 3 (a−8)2 4 分母に√2をかけて,8√2/6=4√2 / 3 5 y=a/xにx=3とy=8を代入すると, 8=a/3より,a=24 y=24/xにx=4を代入して,y=6 6 1/2×1/2=1/4(4分の1) |
| 3秋田県 | 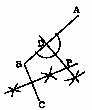 1 3+5=8 1 3+5=82 42+16÷(−4)=42−4=38 3 (5a+3b)円 4 −3a+15b−4a−6b=−7a+9b 5 24a2b2÷3b=8a2b 6 −5√5+2√5=−3√5 7 上式×3+下式×2より,y=−5 x=3,y=−5 8 x2−2x−24=0より,(x−6)(x+4)=0 x=6,−4 9 x2−4=3y+1 (x2−3y−5=0) 10 x(12−x)=20,x<12より,x=2,10 11 ∠x=43×2=86° 12 62×8÷3=96cm3 13 △ABEは二等辺三角形だから,(90−a/2)° 14 20π×72/360=2rπ×120/360より,r=6 15 右上の図 |
7福島県 | 1 (1) 3+4=7 (2) (−5/6)×3/2=−5/4 (3) 3√3−2√3=√3 (4) 6x−9−2x+10=4x+1 2 ∠G=30°より,1辺と両端の角がそれぞれ 等しいから, △ABC≡△IGH (対応をつけてかくこと) |
| 4岩手県 | 1 −1に●をつける 2 (1) 通分して,2/6−3/6=−1/6(−6分の1) (2) 4−12=−8 (3) (x−2)(x−3)=0より, x=2,3 (4) √3(3√3−2√3)=√3×√3=3 [別解] √81−√36=9−6=3 |
8茨城県 | 1番 1 −2 2 12−3=9 3 −12/7+2=2/7 4 9x−6y−10x+8y=−x+2y 5 √48−√27=4√3−3√3=√3 2番 〜おまけ〜 1 (x+5)(x−5) 2 x=2,y=−1 3 x2+4x−21=0より, (x+7)(x−3)=0 x=−7,3 4 4(2x+1)=18より,x=7/4 5 与式=x2+y2=2+3=5 |