15年山形県

～印刷して、紙の上でやってネ！（文字サイズを小にするとＡ４に収まります）～

１

（１）　－２－（－６）

　　　　　　　　　　　　　　　　　　　　　　　　　.

（２）　－	３	×（	４	－	１	）
	７		５		３

　　　　　　　　　　　　　　　　　　　　　　　　　　.

（３）　（２４ｘ^２－１５ｘｙ）÷３ｘ

　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
（４）　√２（３－√２）＋√８

　　　　　　　　　　　　　　　　　　　　　　　　　.
　　

４

　花子さんは，与えられた円について，その中心Ｏを作図するために，下のように，この円と２点で交わる直線をかいた。この続きを考え，コンパスと定規を使って，作図を完成させなさい。

　ただし，作図にお使った線は残しておくこと。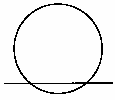

　　　　　　　

５

＜選択問題＞
　下の（Ａ），（Ｂ）のどちらか１問を選び，答えなさい。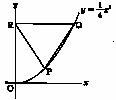

（Ａ）　下の図のように，関数　ｙ＝１/４ｘ２　のグラフ上の，ｘ座標が２である点をＰ，ｘ座標が正でｙ座標が４である点をＱとし，ｙ軸上の点（０，４）をＲとする。このとき，△ＰＱＲの面積を求めなさい。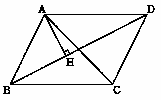

　　　　　　　　　　　　　　　　　　　　　　　　　.

　　

（Ｂ）　下の平行四辺形ＡＢＣＤにおいて，点Ａから対角線ＢＤに垂線をひき，ＢＤとの交点をＨとする。ＡＢ＝５ｃｍ，ＢＨ＝４ｃｍ，ＨＤ＝６ｃｍであるとき，対角線ＡＣの長さは何ｃｍか，求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　.
　

２

　二次方程式　（ｘ＋１）（ｘ－５）＋２ｘ＋２＝０　を解きなさい。解き方も書くこと。

　　　　　　　　　　　　　　　　　　　　　　　　　.
　

３

　数直線上の０の位置にある２点Ｐ，Ｑを，それぞれ次のように移動させる。

　１から６までの目が出る，大，小２つのさいころを同時に１回投げて，点Ｐは，大きいさいころの出た目の数だけ数直線上を右（正の方向）に，点Ｑは，小さいさいころの出た目の数だけ数直線上を左（負の方向）に移動させる。

　このとき，点Ｐと点Ｑとの間の距離が５となる確率を求めなさい。
　ただし，２つのさいころは，どの目が出ることも同様に確からしいものとする。
　　　