 |
（１５） 表面の最短距離 (解答) | 学習日 月 日（ ） | ||||
|
||||||
|
（１５） 表面の最短距離 (解答) | 学習日 月 日（ ） | ||||
|
||||||
| AからBまで,立体の表面上の最短の長さを求めなさい。 (単位はcm) | 円すいの側面上をまわるように,Aからひもをかけるとき,最短の長さを求めなさい。(単位はcm) | ||||
| １ | (1) | 直方体の表面上のA→P→B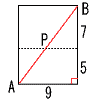 AB2＝92＋122＝225 AB＝√225＝15cm |
２ | (1) | 円すいの表面上のA→A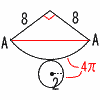 扇形の弧＝底面の円周 ＝4πcmだから 扇形の中心角は90° AB＝8√2cm |
| (2) | 直方体の表面上のA→P→Q→B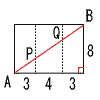 AB2＝102+82＝164 AB＝√164＝2√41cm |
(2) | 円すいの表面上のA→A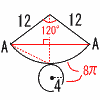 扇形の弧＝底面の円周 ＝8πcmだから 扇形の中心角は120° AB＝正三角形の高さ×2 ＝6√3×2＝12√3cm |
||
| (3) | 立方体の表面上のA→P→B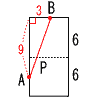 (AとBは辺の中点)AB2＝32＋92＝90 AB＝√90＝3√10cm |
(3) | 円すいの表面上のA→B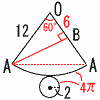 (Bは母線OAの中点)扇形の弧＝底面の円周 ＝4πcmだから 扇形の中心角は60° AB＝正三角形の高さ ＝6√3cm |
||
| ［トップに戻る］ ［問題に戻る］ |
立体の表面上の最短距離 → 展開図で直線を
直方体