| (13) 空間図形への利用2 (解答) | 学習日 月 日( ) | ||||||
|
|||||||
| (13) 空間図形への利用2 (解答) | 学習日 月 日( ) | ||||||
|
|||||||
| 1 | 底面の半径3cm,母線の長さ6cmの円すいについて,それぞれ求めなさい。 | 2 | 底面の1辺が4cm,母線の長さが6cm の正四角すいについて,それぞれ求めなさい。 | |||||||
| (1) | 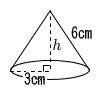 高さh 高さhh2=62−32=27 h=√27=3√3cm |
(1) | 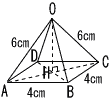 高さOH 高さOHAH= △OAHで OH2=62−(2√2)2=28 OH=√28=2√7cm |
|||||||
| (2) | 体積V V= |
(2) | 体積 V V= |
|||||||
| (3) | 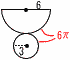 表面積S 表面積SS= =3π+9π=12πcm2 |
(3) | 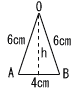 △OABの面積S △OABの面積Sh2=62−22=32 h=√32=4√2 S= |
|||||||
| 3 | 1辺6cmの立方体から,頂点をPとする正三角すいを切り取るとき,それぞれ求めなさい。 | |||||||||
| (1) | 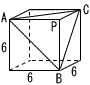 正三角すいP-ABCの体積V 正三角すいP-ABCの体積VV= = |
3 | (3) | 正三角形ABCの面積S 公式を使って
|
||||||
| (2) | 正三角形ABCの1辺の長さ 1辺6cmの正方形の対角線で AB=6√2cm |
(4) | (1)と(3)を利用して,正三角すいP-ABCの高さx(Pから△ABCまでの距離) (1)より,
|
|||||||
| [トップに戻る] [問題に戻る] |