（１１） ２点間の距離 (解答)	学習日　 　 月　 　日（　　）
座標平面上の2点間の距離 → 直角三角形 (ABを斜辺) を作って考える。 　 座標平面上で， 　2点Ａ(1,2)とＢ(3,5)の 　距離を求めなさい。 　　2点ABを斜辺とする直角三角形をつくると, 　　　　三平方の定理より,22＋32＝AB2 　　　　AB＞0だから,AB＝√13　（単位は不要）

印刷して、紙の上でやってネ！　　印刷用

三平方の定理を利用して,2点A,Bの距離を求めなさい。(単位は不要)
１	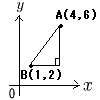Ａ(4,6)とＢ(1,2) ＡＢ2＝(4−1)2＋(6−2)2 　　＝32＋42＝25 　ＡＢ＝√25＝5	２	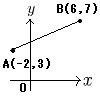Ａ(−2,3)とＢ(6,7) ＡＢ2＝〔6−(−2)〕2 　　　　＋(7−3)2 　　＝82＋42＝80 　ＡＢ＝√80＝4√5
３	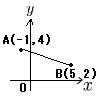点Ａ(−1,4)とＢ(5,2) ＡＢ2＝〔(5−(−1)〕2＋(4−2)2 　　＝62＋22＝40 　ＡＢ＝√40＝2√10	４	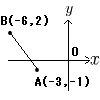Ａ(−3,−1)とＢ(−6,2) ＡＢ2＝〔(−3)−(−6)〕2 　　　　＋〔2−(−1)〕2 　　＝32＋32＝18 　ＡＢ＝√18＝3√2
５	Ａ(−2,−5)とＢ(3,−6) ＡＢ2＝〔3−(−2)〕2＋〔(−6)−(−5)〕2 　　＝52＋(−1)2＝26 　ＡＢ＝√26	６	Ａ(−3,7)とＢ(1,−5) ＡＢ2＝〔1−(−3)〕2＋〔(−5)−7〕2 　　＝42＋(−12)2＝160 　ＡＢ＝√160＝4√10

［トップに戻る］ ［問題に戻る］