（１０） 長方形の折り返し (解答)	学習日　 　 月　 　日（　　）
長方形の折り返し→相似な直角三角形2つ ピタゴラス数 　 点AがBC上の点Fに重なるとき △EBF∽△FCD 相似比を利用 三平方を利用 　 直角三角形の3辺の比 (よく出てくる長さ)

印刷して、紙の上でやってネ！

各図のように長方形を折り返すとき,xの長さを求めなさい。(単位は不要)
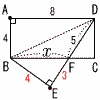１	対角線BDで 　ED＝AD＝8より 　　EF＝8−5＝3 　BE＝BA＝4 　 　△BEFで3辺は,3:4:5 　　x＝5	２	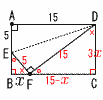点AがBC上の点Fに 　△EBF∽△FCD(相似比1:3) 　△FCDで, 　　(15−x)2＋(3x)2＝152 　　225−30x＋x2＋9x2＝225 　　10x(x−3)＝0で, x＝3
３	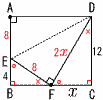点AがBC上の点Fに 　△EBF∽△FCD 　　FD：8＝FC:4より,FD＝2x 　△DFCで, 　　x2＋122＝(2x)2 　　3x2＝144で, x＝√48＝4√3	４	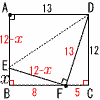点AがBC上の点Fに 　△DFCの3辺は,5:12:13 　　FC＝5より, BF＝8 　△EBFで, 　　x2＋82＝(12−x)2 　　24x＝144−64で, x＝
５	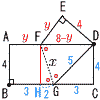点Bが点Dに AF＝yとすると,△EFDで 　y2＋42＝(8−y)2 　16y＝64−16で, y＝3 △DFGは二等辺三角形より 　△DGCは,3:4:5で,HG＝2 △FHGで, x2＝42＋22より, x＝√20＝2√5	６	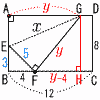点AがBC上の点Fに AG＝yとすると,△GFHで 　(y−4)2＋82＝y2 　8y＝16＋64で, y＝10 　△GFHの3辺は,6,8,10 △EBF∽△FHG (ともに3:4:5) △EFGで, x2＝52＋102より, x＝√125＝5√5

　

［トップに戻る］ ［問題に戻る］