（９） 直角三角形と相似 (解答)	学習日　 　 月　 　日（　　）
相似な3つの直角三角形 相似な2つの直角三角形 (2角相等) 　 相似 △ABC △DBA △DAC

　

１	次の三角形について,x,yの長さを求めなさい。		２	次の長方形について,x,yの長さを求めなさい。
	(1)	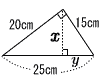x：15＝20：25＝4：5 　　5x＝15×4 　x＝12cm 　y：15＝15：25＝3：5 　　5y＝15×3 　y＝9cm		(1)	3辺の比が 　1:2:√5の直角三角形 　x＝20−8＝12cm 　y＝26−6＝20cm
	(2)	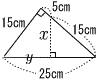x：15＝15：25＝3：5 　　5x＝15×3 　x＝9cm 　（25−y)：20＝15：25 　5(25−y)＝20×3 　25−y＝12で, y＝13cm		(2)	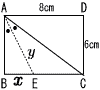AC＝10cm AEは二等分線だから, 　AB:AC＝BE:CE 　6:10＝x:(8−x) 　10x＝6(8−x)で, x＝3cm 　y2＝62＋32で, y＝√45＝3√5cm
３	下の△ABCについて,答えなさい。		４	下の正方形ABCDについて,答えなさい。
	(1)	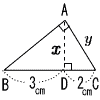△ABCと相似な三角形2つ 　△DBA 　△DAC		(1)	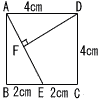AEの長さ 　AE2＝42＋22＝20 　AE＝√20＝2√5cm
	(2)	ADの長さx 　△DAB∽△DACより, x：2＝3：x 　x2＝6で, x＝√6cm		(2)	△DFA∽△ABCとなります。(1)を利用してこの2つの三角形の相似比 　相似比は　4：2√5
	(3)	ACの長さy 　y2＝(√6)2＋22 　y2＝6＋4＝10 　y＝√10cm		(3)	(2)を利用して,△AFDの面積 面積比は, 42:(2√5)2＝16:20＝4:5 　△AFD:△ABC＝△AFD:(×2×4)＝4:5 　△AFD:4＝4:5より, △AFD＝16/5cm2

　

［トップに戻る］ ［問題に戻る］