（７）平面図形への利用２ (解答)	学習日　 　 月　 　日（　　）
正三角形(１辺a) の高さ → h＝ √3 a 2 正三角形(１辺a) の面積 → Ｓ＝ √3 a2 4 １辺4cmの正三角形の 　高さhを求めなさい。 　（解） 三平方の定理より, 　　h2＋22＝42で,h2＝16−4＝12 　　h＞0だから,h＝√12＝2√3cm

　

三平方の定理を利用して,各図の高さhと面積Ｓを求めなさい。
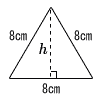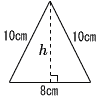１	正三角形 　h2＋42＝82より，h2＝48 　h＝√48＝4√3cm 　Ｓ＝×8×4√3＝16√3cm2		２	二等辺三角形 　h2＋42＝102より，h2＝84 　h＝√84＝2√21cm 　Ｓ＝×8×2√21＝8√21cm2
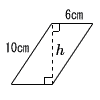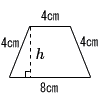３	平行四辺形 　h2＋62＝102より，h2＝64 　h＝√64＝8cm 　Ｓ＝×6×8＝24cm2		４	等脚台形 　h2＋22＝42より，h2＝12 　h＝√12＝2√3cm 　Ｓ＝×(4＋8)×2√3＝12√3cm2
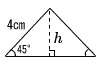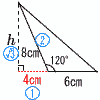５	直角二等辺三角形 　h2＋h2＝42より，h2＝8 　h＝√8＝2√2cm 　Ｓ＝×4√2×2√2＝8cm2		６	鈍角三角形 　h：√3＝8：2 　2h＝8√3で, h＝4√3cm 　Ｓ＝×(4＋6)×4√3＝20√3cm2
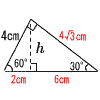７	直角三角形 　h：√3＝4：2 　2h＝4√3で, h＝2√3cm 　Ｓ＝×8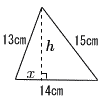×2√3＝8√3cm2		８	鋭角三角形 　h2＝132−x2＝152−(14−x)2 　x＝5で, h＝√132−52＝12cm 　Ｓ＝×14×12＝84cm2 　　(ヒント：先にxを求めよう)

［トップに戻る］ ［問題に戻る］