（３） 定理の証明 (解答)	学習日　 　 月　 　日（　　）
三平方の定理　　 ※ 証明方法は100種類以上もあるらしいよ。 　ピタゴラスの定理 とも呼ばれる 直角三角形では, 　　a2＋b2＝c2

　

各問いに答えて,「三平方の定理」 を証明しなさい。
１	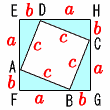右図のように,正方形ABCD(1辺がc)のまわりに,4つの直角三角形(斜辺がc)を並べて,正方形ＥＦＧＨをつくる。		２	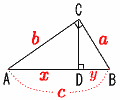右図のように,直角三角形(斜辺がc)の点Cから垂線CDをおろし,AD＝x ,BD＝yとする。
	(1)	正方形ABCDの面積を求めなさい。 　1辺がcだから, c2		(1)	△ABCと相似な三角形をかきなさい。 　△ACD　∽ △ABC 　△CBD　∽ △ABC
	(2)	1つの直角三角形の面積を求めなさい。 　縦と横が a,b だから， ab 2		(2)	(1)より,b：c＝x:b 　よって, b2＝cx
	(3)	正方形EFGHの面積を求めなさい。 　1辺が (a＋b)だから, (a＋b)2		(3)	(1)より,a：c＝y:a 　よって, a2＝cy
	(4)	(1)＋(2)×4＝(3)より, 　a2＋b2＝c2 を証明しなさい。 　c2＋ ab ×4＝(a＋b)2 2 　c2＋2ab＝(a＋b)2 　c2＋2ab＝a2＋2ab＋b2 　よって, a2＋b2＝c2 　　　(証明終わり)		(4)	(2)＋(3)より, 　a2＋b2＝c2 を証明しなさい。 　a2＋b2＝cy＋cx 　　＝c (x＋y)＝c2 　よって，a2＋b2＝c2 　　　　(証明終わり)

［トップに戻る］ ［問題に戻る］