（１１）　円と相似２(解答) 学習日　 　 月　 　日（　　）
円周と交わる線分PA,PBに対して
　相似な三角形ができる

　　△PAC ∽ △PBD
　		 （証明）△PACと△PBDにおいて
　　 ∠A＝∠B(に対する円周角)
∠P＝∠P (共通)
　2角相等で, △PAC∽△PBD
　
相似な三角形を記入して(対応をつけること), 辺の長さx, ∠xの大きさを求めなさい。
１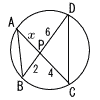
　△PAB∽ △PDC

x：6＝2：4
　x＝6×2÷4＝3
　　　		 ２ 　＝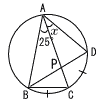

　△ABC∽ △APD

　∠x＝25°(＝)
　
３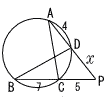
　△PAC∽ △PBD

5：x＝(4＋x)：(7＋5)

　x2＋4x−60＝0より, x＝6		 ４ 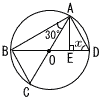点Oは円の中心

　△ABC∽ △AED

　∠x＝90−30＝60°
　　
５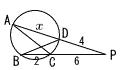
　△PAC∽ △PBD

6：4＝(x＋4)：(2＋6)

　4(x＋4)＝48より, x＝8　		 ６ 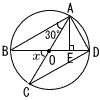点Oは円の中心

　△ABE∽ △ACD

　∠x＝30×2＝60°
　　
７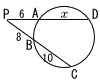
　△PAC∽ △PBD

6：8＝(8＋10）：(6＋x)

　6（6＋x)＝144より, x＝18　　		 ８ 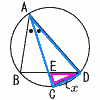AE＝6,EC＝2（●は等しい角)

　△ABE∽△DCE ∽△ACD

2：x＝x：(6＋2)
　x2＝16より, x＝4　
９
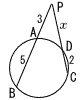　△PAC∽ △PDB

3：x＝(x＋2)：(3＋5)

　x2＋2x−24＝0より, x＝4		 10 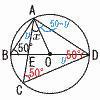AC＝AD,点Oは円の中心
　△ABE∽ △DCE

∠BAE＝yとすると,
　y＋x＋(50−y)＝90
　∠x＝90−50＝40°　

［トップに戻る］ ［問題に戻る］