（９） 円と接線２ (解答)	学習日　 　 月　 　日（　　）
円の接線は， 　　　半径に垂直。 　　OP⊥l  　 円外の点から引いた 　　2本の接線の長さは等しい。 　　PA＝PB

　

１	直線 l,mが円Oに点P,Qで接しているとき,∠x の大きさを求めなさい。		２	円Oが△ABCの各辺に,点P,Q,Rで接しているとき,xの長さを求めなさい。(単位は不要)
	(1)	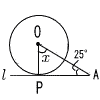∠OPA＝90° 　∠x＝90−25＝65°		(1)	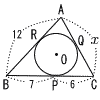BR＝BP＝7 　AR＝AQ＝12−7＝5 CQ＝CP＝6 　x＝AQ＋CQ＝5＋6＝11
	(2)	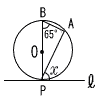∠A＝90° 　∠APB＝90−65＝25° 　∠x＝90−25＝65°		(2)	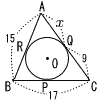BP＝17−9＝8 BR＝BP＝8 　x＝AR＝15−8＝7
	(3)	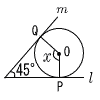∠P＝∠Q＝90° 四角形で, 　∠x＝360−(90 　　　　　＋45＋90) 　　＝360−225＝135°	３	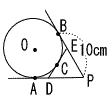右図のように,円Oに3点A,B,Cで接している接線があります。 　空欄をうめて,△DPEの周りの長さ l を求めなさい。
	(4)	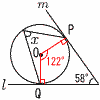∠P＝∠Q＝90° 　∠POQ＝180−58＝122° 　∠x＝122÷2＝61°		(1)	円外から引いた2本の 　　(接線の長さ)は等しいから, 　DA＝( DC ), EB＝( EC ) 　 　PA＝（ PB ）＝10cm
	(5)	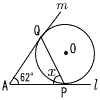円外からの2接線 　AP＝AQで,∠P＝∠Q △APQで, 　∠x＝(180−62)÷2 　　　＝59°		(2)	よって,△DPEの周りの長さは 　l ＝DP＋( DC )＋EP＋( EC ) 　　＝DP＋DA＋EP＋EB 　　＝PA＋( PB )＝( 10 )＋10 　　＝( 20 )cm

［トップに戻る］ ［問題に戻る］