（７） 円周角の定理の逆 (解答)	学習日　 　 月　 　日（　　）
右図で∠APB＝∠AQBのとき, （円周角にあたる部分が等しい） 　　　4点 A,B,P,Qは, 同じ円周上にある。 　別の言い方で, 「四角形PABQは円に内接する」 と言える。

　

１	4点A,B,C,Dが,同じ円周上にあるものには○,ないものには×をつけなさい。		２	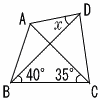右の図で,4点A,B,C,Dがともに同じ円周上にあるとき,∠x の大きさを求めなさい。 弧ABに対する円周角が 　　等しくなればよいから 　∠x＝∠ACB＝35°
	(1)	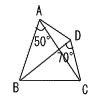∠BAC≠∠BDCより　×
	(2)	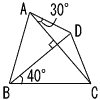∠CAD≠∠CBDより　×	３	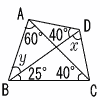右の四角形ABCDで,∠xと∠yの大きさを求めなさい。 ∠ACB＝∠ADB＝40°より 　　4点は同じ円周上 　∠x＝∠BAC＝60° △ABCで, 　∠y＝180−(60＋25＋40)＝55°
	(3)	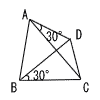∠CAD＝∠CBDより　○
	(4)	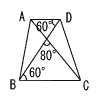∠ADB≠∠ACBより　×	４	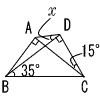∠BAC＝∠BDC＝90°より 　4点は同じ円周上 ∠ABD＝∠ACD＝15° △DBCで, 　∠ACB＝90−35−15＝40° 　∠x＝∠ACB＝40°
	(5)	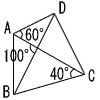∠ADB＝100−60＝40° ∠ADB＝∠ACBより　○	５	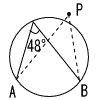右図の円で,∠APBが次のとき,点Pの位置は,ア〜ウのうちのどれか,記号で答えなさい。 　ア　円の内部 　イ　円周上 　ウ　円の外部 ∠APB＝52°のとき,（　ア　） ∠APB＝41°のとき,（　ウ　） ∠APB＝48°のとき,（　イ　）
	(6)	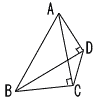∠ACB＝∠ADBより　○

［トップに戻る］ ［問題に戻る］