（１４） 体積比 (解答)	学習日　 　 月　 　日（　　）
相似な空間図形では 　 表面積の比は, 相似比の2乗に等しい。 　　右図で,相似比が1:2 → 表面積の比は 12:22＝1:4 　 体積の比は, 相似比の3乗に等しい。 　　右図で,相似比が1:2 → 体積の比は 13:23＝1:8

　

アとイの空間図形が相似であるとき,相似比・表面積の比 ・体積の比 を求めなさい。
１	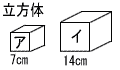相似比 　7:14＝1:2 表面積の比 　12:22＝1:4 体積の比 　13:23＝1:8		２	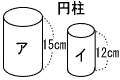相似比 　15:12＝5:4 表面積の比 　52:42＝25:16 体積の比 　53:43＝125:64
３	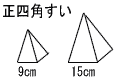相似比 　9:15＝3:5 表面積の比 　32:52＝9:25 体積の比 　33:53＝27:125		４	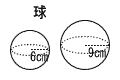相似比 　6:9＝2:3 表面積の比 　22:32＝4:9 体積の比 　23:33＝8:27
次の問いに答えなさい。
１	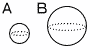球Bの表面積が,球Aの表面積の9倍であるとき		２	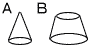１つの円すいを半分の高さの所で水平に2分割するとき
	(1)	ＡとＢの半径の比 表面積比が1:9＝12:32だから 　半径の比は相似比になり, 1:3		(１)	AとBの体積の比 Aと(A＋B)の体積比は,13:23＝1:8だから 　体積比A:B＝1:(8−1)＝1:7
	(2)	Bの体積が108cm3のとき, 　Aの体積 体積比は,13:33＝1:27だから 　A:108＝1:27 　A＝108×1÷27＝4cm3		(2)	元の円すいの体積が72πcm3のとき, 　Bの体積 (A＋B):B＝8:7だから 　72π:B＝8:7 　B＝72π×7÷8＝63πcm3

［トップに戻る］ ［問題に戻る］