 |
（１３） 面積比 (解答) | 学習日 月 日（ ） | ||
|
||||
|
（１３） 面積比 (解答) | 学習日 月 日（ ） | ||
|
||||
| １ | ア,イの図形が相似のとき,次の比を求めなさい。 | ２ | 下の図で,AD:DB＝AE:EC＝1:2 のとき | ||
| (1) | 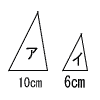 相似比 10:6＝5:3 面積比 52:32＝25:9 |
(1) | 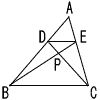 AD:AB＝1:(1＋2)＝1:3 DE:BC＝AD:AB＝1:3 |
||
| (2) | 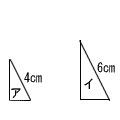 相似比 4:6＝2:3 面積比 22:32＝4:9 |
(2) | △PDE∽△PCB(相似比は1:3)だから 面積比 △PDE:△PCB＝12:32＝1:9 |
||
| (3) | △ADE:△ABC＝12:32＝1:9だから 四角形DBCE:△ABC＝8:9＝x:18 四角形DBCE＝x＝16 |
||||
| (3) | 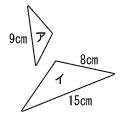 相似比 9:15＝3:5 面積比 32:52＝9:25 |
３ | 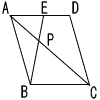 右図のように,平行四辺形ABCDの辺ADの中点をEとするとき,次の面積比を求めなさい。 |
||
| (4) | 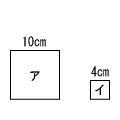 相似比 10:4＝5:2 面積比 52:22＝25:4 |
(1) | AD=BCより,AE:BC＝1:2 △APE∽△CPBだから △APE:△CPB＝12:22＝1:4 |
||
| (5) | 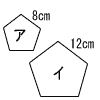 相似比 8:12＝2:3 面積比 22:32＝4:9 |
(2) | △ABPと△CBPは高さが等しいから, 面積は底辺に比例する。 △APE∽△CPB(相似比は1:2)より 底辺の比 AP:CP＝1:2 △ABP:△CBP＝1:2 |
||
| (6) | 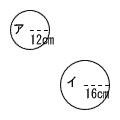 相似比 12:16＝3:4 面積比 32:42＝9:16 |
(3) | △APE:△CPB:△APB＝1:4:2となるから △APB＝2のとき 四角形EPCD＝2＋4−1＝5 △ABP:四角形EPCD＝2:5 |
||
| ［トップに戻る］ ［問題に戻る］ |
相似な図形では,面積の比は,相似比の2乗に等しい。