 |
（１２） 中点連結定理 (解答) | 学習日 月 日（ ） | |||||||||||
|
|||||||||||||
|
（１２） 中点連結定理 (解答) | 学習日 月 日（ ） | |||||||||||
|
|||||||||||||
| １ | 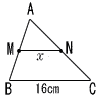 点MとNが中点のとき,xの長さを求めなさい。中点連結定理より x＝16÷2＝8cm |
２ | 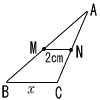 点MとNが中点のとき,xの長さを求めなさい。中点連結定理より x＝2×2＝4cm |
|
| ３ | 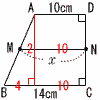 点MとNが中点のとき,xの長さを求めなさい。ＡからＤＣに平行な線分を 引くとよい。 中点連結定理より x＝2＋10＝12cm |
４ | 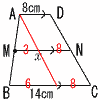 AD//MN//BCで,点Mが中点のとき,xの長さを求めなさい。ＡからＤＣに平行な線分を 引くとよい。 (ＤからＡＢに平行線も可) 中点連結定理より x＝3＋8＝11cm |
|
| ５ | 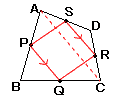 四角形ABCDの4辺それぞれの中点をP,Q,R,Sとすると,四角形PQRSはどんな四角形になりますか。AとCを結ぶと △ABCで,PQ//＝  AC△ACDで,SR//＝ ACよって,PQ//＝SR 1組の対辺が平行で等しいから, 平行四辺形 |
７ | (1) | 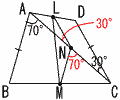 AB＝CDである四角形ABCDで,AD,BC,ACの中点をL,M,Nとすると,△LMNはどんな三角形になりますか。△ABCで,NM＝ AB△ACDで,NL＝ CDAB＝CDだからNM＝NL よって, 二等辺三角形 |
| ６ | 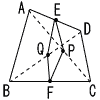 右図のように,四角形ABCDの辺ADの中点をE,辺BCの中点をFとする。さらに,対角線ACの中点をP,対角線BDの中点をQとすると,四角形EQFPはどんな四角形になりますか。 △DABで,EQ//AB △CABで,PF//AB よってEQ//PF …ア △BDCで,QF//DC △ADCで,EP//DC よって,QF//EP …イ ア,イより,2組の対辺が平行だから,平行四辺形 |
(2) | ∠BAC=70°,∠DCA=30°のとき,次の角の大きさを求めなさい。 △NLMで, ∠ANM＝180−70＝110° よって,∠LNM＝30＋110 ＝140° △ＮLM(二等辺三角形)で, ∠MLN＝(180−140)÷2 ＝40÷2＝20° |
|
| ［トップに戻る］ ［問題に戻る］ |
三角形の2辺の中点を結ぶ線分（中点連結）は, 底辺に平行で,長さは半分。
BC