 |
（１１） 平行線と比２ (解答) | 学習日 月 日（ ） | ||||||
|
||||||||
|
（１１） 平行線と比２ (解答) | 学習日 月 日（ ） | ||||||
|
||||||||
| １ | 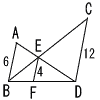 右図で,AB//CD//EF である。次の空欄をうめなさい。 |
２ | 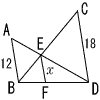 右図で,AB//CD//EF である。次の空欄をうめて,EFの長さを求めなさい。 |
||
| (1) | △DEF ∽ △DAB 相似比は 4:6＝2:3 |
(1) | △ABE ∽ △DCE 相似比は 12:18＝2:3 |
||
| (2) | △BEF ∽ △BCD 相似比は 4:12＝1:3 |
(2) | △BEF ∽ △BCD (1)より, BE:BC＝2:(2＋3)＝2:5 |
||
| (3) | △ABE ∽ △DCE 相似比は 6:12＝1:2 |
(3) | (2)より, x:18＝2:(2＋3)＝2:5 5x＝36 x＝7.2 (36/5も可) |
||
| ３ | 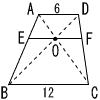 右図のように,台形ABCDの対角線の交点Oから平行線EFをひくとき,空欄をうめて,EFの長さを求めなさい。 |
４ | 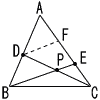 右の△ABCの辺上で,AD:DB=1:1となるを点D, AE:EC＝2:1となる点Eとする。 空欄をうめ,BP:PE を求めなさい。 ［ヒント］ DからBEに平行線DFをひくと, FはAEの中点となる。 （次ページの 『中点連結定理』 より） |
||
| (1) | △ADO ∽ △CBO 相似比は 6:12＝1:2 |
||||
| (2) | (1)より AO:CO＝1:2 |
||||
| (3) | △AEO ∽ △ABC 相似比は 1：(1＋2)＝1:3 |
(1) | △ABEで DF:BE＝1:2 |
||
| (4) | (3)より,EO:12＝1:3 3EO＝12 EO=4 |
(2) | △CDF PE:DF＝1:2 |
||
| (5) | 同様に,FO:12＝1:3 3FO＝12 FO=4 |
(3) | (1),(2)より PE:DF:BE＝1:2:4 |
||
| (6) | (4)＋(5)より EF＝4＋4＝8 |
(4) | (3)より BP:PE＝(4−1):1＝3:1 |
||
| ［トップに戻る］ ［問題に戻る］ |
右図で,AB//CD//EF のとき
相似な三角形を見つけましょう。
