 |
（８）相似の利用 (解答) | 学習日 月 日（ ） | ||||||||||||||
|
||||||||||||||||
|
（８）相似の利用 (解答) | 学習日 月 日（ ） | ||||||||||||||
|
||||||||||||||||
| １ | 下の直角三角形ABCについて答えなさい。 | ２ | 二等辺三角形ABCで,BC=BDのとき | ||
| (1) | 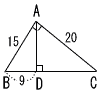 △ABCと相似な三角形を2つ答えなさい。△ABC ∽ △DBA △ABC ∽ △DAC |
(1) | 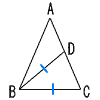 △ABCと相似な三角形を答えなさい。△ABC ∽ △BCD ( △ABC ∽ △BDCも可 ) |
||
| (2) | (1)より, ADの長さを求めなさい。 △DBA∽△DACより AB:CA＝BD:AD 15:20＝9:AD AD＝20×9÷15＝12 |
(2) | (1)より, BC2＝AB×CDを証明しなさい。 △ABC∽△BCDより AB:BC＝BC:CD よって, BC2＝AB×CD |
||
| ３ | 1辺が15の正三角形を図のように折り返しました。 | ４ | 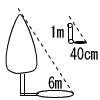 ある木の高さを調べるため,木の影の長さを測ったら6mでした。同時に,1mの棒の影を測ったら40cmでした。木の高さを求めなさい。 太陽の光はまっすぐ進むから, 三角形の相似を利用すればよい。 木の高さをxmとすると, x:1＝6:0.4 x＝1×6÷0.4＝60÷4＝15m |
||
| (1) | 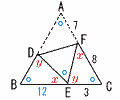 △DBEと相似な三角形を答えなさい。x＋y＝120°で 2組の角が等しくなって △DBE∽△ECF |
||||
| (2) | (1)より, ADの長さを求めなさい。 △DBE∽△ECFより DB:EC＝BE:CF DB:3＝12:8で,DB＝3×12÷8＝4.5 よって, AD＝15−4.5＝10.5 |
||||
| ［トップに戻る］ ［問題に戻る］ |
相似条件
3組の辺の比がそれぞれ等しい。
