（７）相似の証明２ (解答)	学習日　 　 月　 　日（　　）
2つの三角形が相似になるための条件 相似の証明 3組の辺の比がすべて等しい 2組の辺の比と,その間の角がそれぞれ等しい 2組の角がそれぞれ等しい △　　　　と△　　　　において 　 　　　＝　　　 (理　由) …�@ 　　　＝　　　 (理　由) …�A 　　　＝　　　 (理　由) …�B �@�A�Bより, 　相似条件　で 　△　　　∽△　　　.

　

図を参考にして空欄をうめ,次の三角形が相似であることを証明しなさい。
１	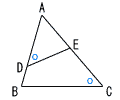△ABC∽△AEDである。 ［証明］ △ABCと△AEDにおいて ∠ACB＝∠ADE (仮　定) ∠BAC＝∠EAD (共　通) 相似条件(　2組の角　) 　　　がそれぞれ等しいから, 　△ABC ∽ △AED	２	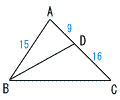△ABC∽△ADBである。 ［証明］ △ABCと△ADBにおいて AB：AD＝ 15: 9＝5:3 (仮　定) AC：AB＝ 25:15＝5:3 (仮　定) ∠BAC＝ ∠DAB　　 (共　通) 相似条件(2組の辺の比と,その間の角) 　　　がそれぞれ等しいから, 　△ABC ∽ △ADB
３	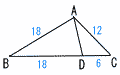△ABC∽△DACである。 ［証明］ △ABCと△DACにおいて BC：AC＝ 24:12＝2:1 (仮　定) AC：DC＝ 12: 6＝2:1 (仮　定) 　∠ACB＝ ∠DCA　(共　通) 相似条件(2組の辺の比と,その間の角) 　　　がそれぞれ等しいから, 　△ABC ∽ △DAC	４	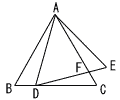△ABCと△ADEが正三角形のとき 　△ABD∽△AEFである。 ［証明］ △ABDと△AEFにおいて ∠ABD＝∠AEF＝60° (仮　定) ∠BAD＝∠EAF＝60°−∠DAC 相似条件((　2組の角　) 　　　がそれぞれ等しいから, 　△ABD ∽ △AEF

［トップに戻る］ ［問題に戻る］