（11） y＝ax2 の利用 ４ (解答) 学習日　 　月　　 日（　　　）
座標平面の放物線
放物線 y＝3x2 上の点Pは,x座標をaとして,
　Ｐ(a，3a2) と表される
　
１ 　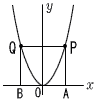放物線y＝x2上にy軸対称な2点Ｐ,Ｑをとるとき,


 ２ 　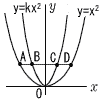2つの放物線y＝x2 とy＝kx2があり,x軸と平行な線分と4点A,B,C,Dで交わるとき,
(1) 　点Pのx座標をaとするとき,点Qの座標をaの式で表しなさい。

　Q(−a,a2)
　		 (1) 　点Cのx座標をaとするとき,点AとCの座標を,aを使って表しなさい。

　A(−2a,4a2), C(a,ka2)
　
(2) 　四角形PQBAが正方形になるとき,aの値を求めなさい。

PA＝a2,PQ＝2aだから,
　a2＝2a
a(a−2)＝0 より, a＝2　(a＝0は不適)　		 (2) 　AB＝BC＝CDとなるとき,kの値を求めなさい。

点Ａと点Ｃのy座標は等しくなるから,
　4a2＝ka2
よって, k＝4　
３ 　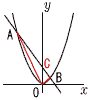放物線 y＝x2 と直線 y＝−2x＋3が2点A,Bで交わるとき,
　		 ４ 　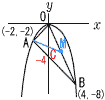関数 y＝ax2 上に,2点A(−2,−2),B(4,−8)があるとき,
　
(1) 　2点A,Bの座標を求めなさい。
｛ y＝x2 で, x2＝−2x＋3
y＝−2x＋3
　(x＋3)(x−1)＝0より, x＝−3,1
よって, A(−3,9)　B(1,1)　　		 (1) 　△OABの面積を求めなさい。

2つの三角形に分けて考える。
Cは (0,−4)だから,
　△OAB＝△OAC＋△OBC
　　＝×4×(4＋2)＝ 12　　
(2) 　△OABの面積を求めなさい。

2つの三角形に分けて考える。
　底辺OCが共通で,C(0,3)だから,

　△OAB＝△OAC＋△OBC
　　＝×3×(1＋3)＝ 6　　		 (2) 　点A通り,△OABを2等分する直線の式を求めなさい。
線分OBの中点はM(2,−4)で,
　AMが2等分する直線となる。
傾き＝ (−4)−(−2) ＝ −2 ＝− 1
2−(−2) 4 2
よって, y＝−x−3　

［トップに戻る］ ［問題に戻る］