（１２）２次方程式の利用３(解答) 学習日　　月　　日（　　）
　いろいろな問題への利用
　 物を秒速100mの速さで真上に打ち上げるとき,
　　 x 秒後の高さyは, y＝100x－5x2 で表される。
　　 3秒後の高さを求めなさい。
　式にx＝3 を代入して,
　y＝100×3－5×32
　　＝300－45＝ 255m
　
方程式を作って,それぞれの解を求めなさい。
１ 　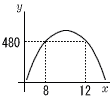物を秒速100mの速さで真上に打ち上げるとき,x秒後の高さyは, y＝100x－5x2…ア で表されます。

(1) 高さが480mになるのは何秒後ですか。

アにy＝480を代入して,480＝100x－5x2
移項して整理すると,x2－20x＋96＝0
(x－8)(x－12)＝0より、x＝8，12
　　(答) 8秒後と12秒後

(答えが2つあるのは,昇るときと落ちるとき)

(2) 再び地上にもどるのは何秒後ですか。

地上は高さ0mだから,アにy＝0を代入して,
　0＝100x－5x2
移項して整理すると,5x(x－20)＝0
　x＝20　　(答) 20秒後　		 ２ 　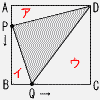1辺10cmの正方形の辺上を,点PはAからBまで,点QはBからCまで,どちらも毎秒1cmの速さで動きます。PとQが同時に出発するとき,

(1) 2秒後の△PQDの面積を求めなさい。
ア＝×2×10＝10
イ＝×2×8＝8
ウ＝×8×10＝40
　△PQD＝102－(10＋8＋40)＝ 42cm2

(2) △PQDの面積が38cm2になるのは何秒後ですか。
ア＝×x×10＝5x
イ＝×x×(10－x)＝5x－x2
ウ＝×(10－x)×10＝50－5x
　△PQD＝102－(5x＋5x－x2＋50－5x)
　　＝x2－5x＋50＝38
移項して整理すると,x2－10x＋24＝0
　(x－4)(x－6)＝0より,x＝4,6
　　　(答) 4秒後と6秒後　
３
　n角形の対角線の本数は, n(n－3) と表せ
2
る。対角線が20本となるのは何角形ですか。

　n(n－3) ＝20
2
移項して整理すると,n2－３n－40＝0
　(n－8)(n＋5)＝0より,n＝8,－5
n＞0だから,n＝8
　　(答) 八角形		 ４ 　正の整数xがあります。x2をxより4小さい数で割ると,商が20で,余りが5になりました。xを求めなさい。

　x2÷(x－4)＝20余り5
よって,x2＝20(x－4)＋5
移項して整理すると,x2－20x＋75＝0
　(x－5)(x－15)＝0より,x＝5,15
余りが5だから,x－4＞5
つまりx＞9で, x＝15　 　

［トップに戻る］ ［問題に戻る］