| (18)式の利用3 (解答) | 学習日 月 日( ) | |||||
|
||||||
| (18)式の利用3 (解答) | 学習日 月 日( ) | |||||
|
||||||
| 1 | 奇数×奇数=奇数 (証明)m.nを整数とすると, 奇数×奇数=(2m+1)(2n+1) =4mn+2m+2n+1 =2(2mn+m+n)+1 → 奇数 |
2 | 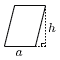 平行四辺形(底辺a,高さh) 平行四辺形(底辺a,高さh)面積 = a×h = ah |
| 3 | 連続する3つの整数の和は3の倍数 (証明)中央の整数をnとすると, 3数の和=(n−1)+n+(n+1) = 3n → 3の倍数 |
4 | 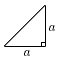 直角二等辺三角形(等辺a) 直角二等辺三角形(等辺a)面積 = = |
| 5 | 連続する2つの偶数の2乗の差は4の倍数 (証明)nを整数とすると, 差=(2n+2)2−(2n)2 =(4n2+8n+4)−4n2 =4(2n+1) → 4の倍数 |
6 | 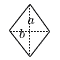 ひし形(対角線aとb) ひし形(対角線aとb)面積 = a×b÷2 = |
| 7 | 3で割るとき,1余る数+2余る数=3の倍数 (証明)m.nを整数とすると, 和=(3m+1)+(3n+2) =3m+3n+3 =3(m+n+1) → 3の倍数 |
8 | 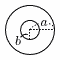 ドーナツ形(半径aとb) ドーナツ形(半径aとb)面積 = π×a2−π×b2 = π(a2−b2) |
| 9 | 連続する2つの偶数の積+1=(奇数)2 (証明)nを整数とすると, 和=(2n)(2n+2)+1 =4n2+4n+1 =2(2n2+2n)+1 → 奇数 |
10 | 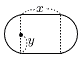 トラック形(長辺x,半径y) トラック形(長辺x,半径y)面積 = x×2y+π×y2 = 2xy+πy2 |
| [トップに戻る] [問題に戻る] |