（６） 直角三角形の合同２	学習日　 　 月　 　日（　　）
直角三角形の合同条件 　直角三角形の, 　　斜辺と１つの鋭角が 　　　それぞれ等しい。 　直角三角形の, 　　斜辺と他の１辺が 　　　それぞれ等しい。

印刷して、紙の上でやってネ！　　印刷用

空欄をうめて,次のことがらを証明しなさい。
下の各図において､青印は仮定を、赤印は結論を表している。
１	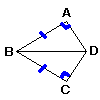AB＝BCで,∠Ａ＝∠Ｃ＝90°のとき,△ABDと△CBDは合同である ［証明］ △ABDと △CBD において, 　 ∠A ＝　∠B　　＝90°（仮定） BD ＝　BD　　　　（　共通　） AB ＝　CB　　　　（　仮定　） 合同条件：直角三角形の 　(　斜辺と他の１辺　) 　　　がそれぞれ等しいから, 　△ABD≡ △CBD	２	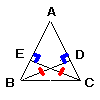二等辺三角形ABCの点BとCから対辺に垂線BD,CEをおろすとき,BD＝CEとなる ［証明］ △ABDと △ACE において, 　 ∠ADB＝ 　∠AEC ＝90°（仮定） AB＝ 　　AC　　 （　仮定　） ∠BAD＝ 　∠CAE　 （　共通　） 合同条件：直角三角形の 　(　斜辺と1つの鋭角　) 　　　がそれぞれ等しいから, 　△ABD≡ △ACE で, BD＝ CE
３	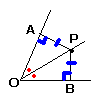点Pから直線OA,OBまでの距離が等しいとき,点Pは∠AOBの二等分線上にある ［証明］ △POAと ΔPOB において, 　 ∠PAO＝ 　∠PBO　＝90°（仮定） PO＝ 　　PO　　　（　共通　） PA＝ 　　PB　　　（　仮定　） 合同条件：直角三角形の 　(　斜辺と他の１辺　) 　　　がそれぞれ等しいから, 　△POA≡ ΔPOB で, ∠POA＝ ∠POB	４	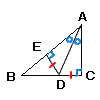直角三角形ABCの∠Aの二等分線と辺BCの交点をDとし,Dから辺ABに垂線DEを引くとき,DE＝DCである ［証明］ △ADEと △ADC において, 　 ∠Ｅ＝ 　 ∠C　　＝90°（仮定） AD＝ 　　AD　　　（　共通　） ∠DAE＝ 　∠DAC　　（　仮定　） 合同条件：直角三角形の 　(　斜辺と1つの鋭角　) 　　　がそれぞれ等しいから, 　△ADE≡ △ADC で, DE＝ DC

［トップに戻る］ ［問題に戻る］